Месяц: Февраль 2024

60⁰

4)Տրված է DE II BC, BD = DE: Գտեք <EBC-ն, եթե <ADE=50⁰

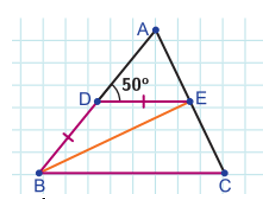
125⁰

5)Տրված է AB II CD, <BED=80^o , <EDC=30^o: Գտեք < ABC անկյունը։

20⁰

Աքսիոմն այնպիսի ճշմարտություն է, որը չի ապացուցվում: Յուրաքանչյուր գիտություն ունի իր աքսիոմները, որոնց վրա են հիմնվում բոլոր հետագա պնդումներն ու ապացույցները:

Զուգահեռ ուղիղների աքսիոմը.

Տրված ուղղի վրա չգտնվող կետով անցնում է այդ ուղղին զուգահեռ միայն մեկ ուղիղ:

Երբեմն այս աքսիոմն համարում են զուգահեռ ուղիղների հատկություն, սակայն այս աքսիոմի վրա են հիմնված շատ պնդումների ապացույցներ երկրաչափության մեջ:  

Զուգահեռ ուղիղների այլ հատկություններ.

1. Եթե երկու ուղիղներ զուգահեռ են երրորդ ուղղին, ապա դրանք զուգահեռ են:

2. Եթե ուղիղը հատում է զուգահեռ ուղիղներից մեկը, ապա այն հատում է նաև երկրորդը:

Առաջադրանքներ․

1)Երկու զուգահեռ ուղիղները հատողով հատելիս խաչադիր անկյունների գումարը 240^o է։ Գտեք այդ անկյունների կից անկյունները։ 

240:2=120

120:2=60

2)Նկարում a, b և c ուղիղները հատած են d հատողով, < 1 = 42 ^o , < 2 = 140^o , < 3 = 138^o : a, b և c ուղիղներից որո՞նք են զուգահեռ։

<1+<3=180 => a c

3)Գտեք բոլոր անկյունները, որոնք առաջանում են երկու՝ a և b զուգահեռ ուղիղները c հատողով հատելիս, եթե՝

բ)անկյուններից մեկը 150⁰ է

3=150

4=30

ա)անկյուններից մեկը 70⁰ -ով մեծ է մյուսից։

4=55

4=125

4)Ըստ նկարի տվյալների՝ գտեք <1 -ը։ 

88

5)ABC անկյունը 70⁰ է, իսկ BCD անկյունը՝ 110⁰։ AB և CD ուղիղները կարո՞ղ են, արդյոք, լինել՝

ա)զուգահեռ

բ)հատվող+

Խորանարդների գումարը արտադրիչների վերլուծելու համար օգտագործվում է

a³ + b³ = (a + b) (a² — ab + b²)            ( 1 )

նույնությունը, որը կոչվում է խորանարդների գումարի բանաձև:

Օրինակ 1: Արտադրիչների վերլուծենք 27x³ + y³ բազմանդամը:

Տվյալ բազմանդամը հնարավոր է ներկայացնել երկու արտահայտությունների խորանարդների գումարի տեսքով.

27x³ + y³ = (3x)³ + y³:

Կիրառելով (1) բանաձևը կստանանք.

(3x) ³ + y³ = (3x + y) (9x² — 3xy + y²):

Եվ այսպես՝

27x³ + y³ = (3x + y) (9x² — 3xy + y²):

Խորանարդների տարբերությունը արտադրիչների վերլեւծելու համար օգտագործվում է

a³ — b³ = (a – b) (a² + ab + b²)            ( 2 )

նույնությունը, որը կոչվում է խորանարդների տարբերության բանաձև:

Օրինակ 2: Արտադրիչների վերլուծենք m⁶ — n³ բազմանդամը:
Տվյալ բազմանդամը ներկայացնենք երկու արտահայտությունների խորանարդների տարբերության տեսքով և կիրառենք (2) բանաձևը: Կստանանք՝

m⁶ — n³ = (m²)³ — n³ = (m² — n) (m⁴ + m²n + n²):

Առաջադրանքներ

1)Միանդամը ներկայացրո՛ւ խորանարդի տեսքով․

125-5³

8=2³

27x³=(3x)³

64y³=(4y)³

M³y³=(my)³

A⁶b³=(a²b)³

(xy²)³

2)Հաշվի՛ր օգտվելով Խորանարդների գումարի բանաձևից՝
a³ + b³ = (a + b) (a² — ab + b²)            ( 1 )

(x+2)(x²-2x+2²)

(3+a)(3²-3a+a²)

4)Հաշվի՛ր օգտվելով Խորանարդների գումարի բանաձևից՝
(a + b) (a² — ab + b²)=a³ + b³

 Աշխատանք դասարանում 

Կարդա՛ բանաստեղծությունը, կատարի՛ր առաջադրանքները:

Գարնան քաղաքում

 Լցվում է փողոցն աղմուկ ուշարժում,

Դալուկ դեմքերին ծաղկում է ժպիտ,

Փայլում են տներն արևի փոշում,

Երկինք են պարզվում ծառերը վտիտ…

Դեռ չչորացած բուլվարի վրա

Ճչում են զվարթ մանուկն՚երն արդեն.

Բոլոր խոսքերը խորհուրդ են հիմա

Եվ հայացքները նետ են իրար դեմ…

Մայթի քարերը հարազատ են քեզ —

Քեզ նոր է թվում երգը հնամյա.

Ազատ է հոգիդ, անչար է և հեզ,

Եվ տխրությունդ անուշ է հիմա…

Ժպտուն աղջիկներ՝ ծաղիկների պես,

Տիկիններ շքեղ և ծիծաղելի —

Բոլորը հիմա սիրելի են քեզ,

Ամեն ինչ անուշ խորհրդով էլի…

Մեռած սրտերն էլ, ծաղիկների պես,

Բացվում են հիմա արևի փոշում.

Մի քաղցր հուզում արբեցնում է քեզ,

Ու, հոգսով մղված՝ հոգսդ չես հիշում…

Օրհնությո՜ւն քեզ, ե՛րգ, և երա՛զ, և սե՛ր,

Օրհնությո՜ւն քեզ, կյա՛նք անուշ և անհուն,

Օրհնությո՜ւն և քե՛զ, տանջանքի գիշեր:

Եվ երկունք, և մահ — փա՛ռք և օրհնությո՛ւն…

• Դուրս գրի՛ր անհասկանալի բառերը և բառարանի օգնությամբ բացատրիր: Անհուն-Հուն չունեցող
• Բանաստեղծության մեջ ինչպես է նկարագրվում գարնան քաղաքը, գրավոր ներկայացրու:Այնտեղ ասում էր, որ փողոցը լցված էր աղմուկով և մարդկանց դեմքերին բացվում է ժպիտ։