շրջանագծի շոշափոխ

Եթե շրջանագծի կենտրոնի հեռավորությունն ուղղից հավասար է շրջանագծի շառավղին, ապա շրջանագիծն ու ուղիղը ունեն մեկ ընդհանուր կետ:

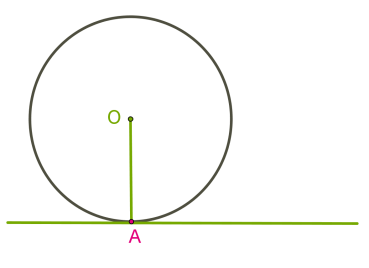
Այդ դեպքում ուղիղն անվանում են շրջանագծի շոշափող:

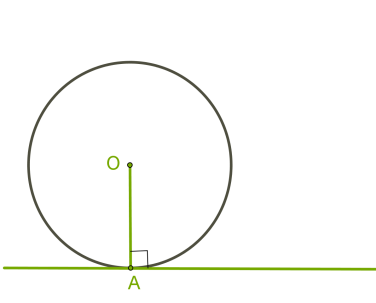
Եթե ուղիղը շրջանագծի հետ ունի մեկ ընդհանուր կետ, ապա այն կոչվում է շրջանագծի շոշափող:

Շրջանագծի շոշափողը ուղղահայաց է շոշափման կետից տարված շառավղին:

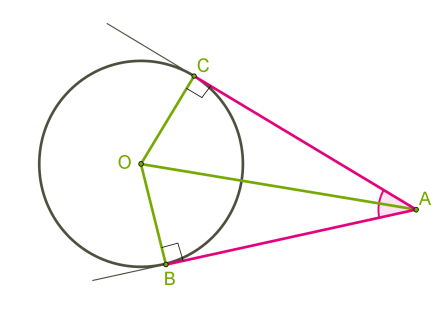
Եթե միևնույն կետից շրջանագծին տարված են երկու շոշափողներ, ապա

ա) շոշափման կետերի հեռավորությունները տրված կետից հավասար են,

բ) շրջանագծի կենտրոնով և տրված կետով անցնող ուղիղը կիսում է շոշափողների կազմած անկյունը:

Առաջադրանքներ․

1)Ճիշտ են արդյո՞ք հետևյալ պնդումները:

ա)Եթե ուղիղը շրջանագծի շոշափողն է, ապա այն ունի շրջանագծի հետ երկու ընդհանուր կետ:

• ոչ+
• այո

բ)Եթե ուղիղը շրջանագծի հետ ունի ընդհանուր կետ, ապա այն հանդիսանում է շրջանագծի հատող:

• այո
• ոչ+

գ)Ուղիղն ու շրջանագիծը կարող են ունենալ միայն երկու ընդհանուր կետ:

• ոչ
• այո+

2)Տրված է՝ ∢CAO=29°

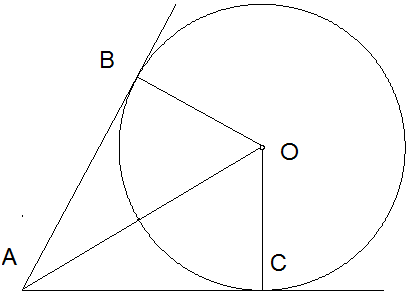
Հաշվիր՝

∢ABO=90

∢COA=90

3)Տրված է A անկյունը, որի կողմերը շոշափում են O կենտրոնով և 6 սմ շառավղով շրջանագիծը: Հաշվիր OA հատվածի երկարությունը, եթե ∡A=60°:

4)Շրջանագծին A, C և E կետերում տարված են AB, BD և DE շոշափողները, իսկ AB=8 սմ: Որոշիր ACE եռանկյան պարագիծը:

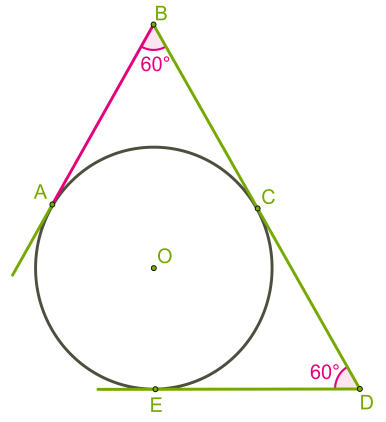
180-60:2=60

3×8=24

Լրացուցիչ աշխատանք (տանը).