հանրահաշիվ

Գիտենք, որ իրական թվերի երկրաչափական մոդելը թվային ուղիղն է: Ցանկացած իրական թիվ թվային ուղղի վրա ունի իր դիրքը: Հիմա կպարզենք, թե ինչպես են թվային ուղղի վրա պատկերվում թվային միջակայքերը: Կօգտագործենք հետևյալ նշանակումները. 

Անհավասարությունների և ծայրակետերի նշանակումներ	Բազմությունների նշանակումներ
≤ կամ ≥ ∙ (ծայրակետն ընդգրկված է)	[ և]քառակուսի փակագծեր
< կամ > о (ծայրակետն ընդգրկված չէ)	( և )կլոր փակագծեր

Գոյություն ունեն թվային ուղղի վրա բազմությունների 4 տեսակի նշանակումներ:

Ամբողջ թվային ուղիղը նշանակվում է այսպես՝ (−∞;∞)։

Եթե x թիվը միաժամանակ բավարարում է x>−4 և x<5 անհավասարություններին, ապա այն բավարարում է −4<x<5 երկկողմանի անհավասարությանը:

−4<x<5 երկկողմանի անհավասարությանը բավարարող բոլոր թվերի բազմությունը անվանում են թվային միջակայք և նշանակում են այսպես՝ (−4;5):

Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «−4, 5 ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):

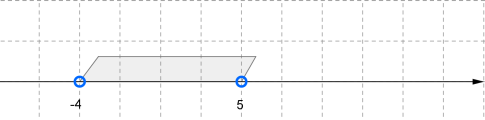
Դիտարկենք ուրիշ միջակայքեր:

−4≤x≤5 կամ x∈[−4;5]: Կարդում ենք՝ «−4, 5 հատված», կամ «փակ միջակայք»: Նկատենք, որ հատվածի ծայրակետերը ընդգրկված են (սևացված են):

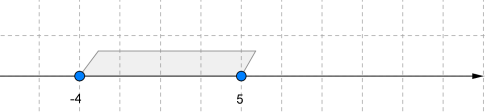
−4≤x<5 կամ x∈[−4;5): Կարդում ենք՝ «−4, 5 կիսաինտերվալ», կամ «կիսաբաց միջակայք»: Նկատենք, որ կիսաինտերվալի ծայրակետերից մեկը՝ −4 -ը ընդգրկված է (սևացված է), իսկ մյուսը՝ 5 -ը ընդգրկված չէ (սևացված չէ):

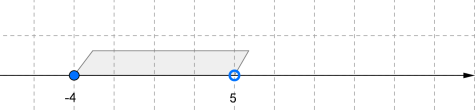
−4<x≤5 կամ x∈(−4;5]: Սա ևս կիսաինտերվալ է՝ բաց ձախ ծայրակետով:

Առաջադրանքներ․

1)Անվանեք թվային բազմությանը պատկանող բոլոր ամբողջ թվերը՝

ա)[-3;1]

բ)(-3;1)

գ)[-3;1)

դ)(-3;1]

ե)[-2;3]

զ)(-2;3)

է)[-2;3)

ը)(-2;3]

2)Պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա)[3;5]

բ)(3;5)

գ)[3;5)

դ)(3;5]

ե)[-2;+∞)

զ)(-2;+∞)

է)(-∞;-2)

ը)(-∞;-2]

3)Պատկանու՞մ է արդյոք -2 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)[-3;0]

բ)(-2;3)

գ)(-∞;-2]

դ)(-3;+∞)

ե)N

զ)Z

է)Q

ը)R

4)Անվանեք թվային բազմությանը պատկանող երեք ամբողջ թվեր՝

ա)[0;+∞)

բ)(0;+∞)

գ)(-∞;1)

դ)(-∞;1]

5)Գրառեք նշանակումը և պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա)2-ից 4 փակ միջակայքի (հատվածի)

բ)2-ից 4 բաց միջակայքի

գ)2-ից 4 կիսաբաց միջակայքի՝ 4-ը ներառած

դ)2-ից 4 կիսաբաց միջակայքի՝ 2-ը ներառած

ե)5-ից +∞ միջակայքի

զ)5-ից +∞ կիսաբաց միջակայքի

է) -∞-ից 0 միջակայքի

ը) -∞-ից 0 կիսաբաց միջակայքի

6)Պատկանու՞մ է արդյոք 2/3 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)(0;1]

բ)[1;2]

գ)(-∞;2/3]

դ)(2/3;+∞)

ե)N

զ)Z

է)Q

ը)RԳիտենք, որ իրական թվերի երկրաչափական մոդելը թվային ուղիղն է: Ցանկացած իրական թիվ թվային ուղղի վրա ունի իր դիրքը: Հիմա կպարզենք, թե ինչպես են թվային ուղղի վրա պատկերվում թվային միջակայքերը: Կօգտագործենք հետևյալ նշանակումները. 

Անհավասարությունների և ծայրակետերի նշանակումներ	Բազմությունների նշանակումներ
≤ կամ ≥ ∙ (ծայրակետն ընդգրկված է)	[ և]քառակուսի փակագծեր
< կամ > о (ծայրակետն ընդգրկված չէ)	( և )կլոր փակագծեր

Գոյություն ունեն թվային ուղղի վրա բազմությունների 4 տեսակի նշանակումներ:

Ամբողջ թվային ուղիղը նշանակվում է այսպես՝ (−∞;∞)։

Եթե x թիվը միաժամանակ բավարարում է x>−4 և x<5 անհավասարություններին, ապա այն բավարարում է −4<x<5 երկկողմանի անհավասարությանը:

−4<x<5 երկկողմանի անհավասարությանը բավարարող բոլոր թվերի բազմությունը անվանում են թվային միջակայք և նշանակում են այսպես՝ (−4;5):

Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «−4, 5 ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):

Դիտարկենք ուրիշ միջակայքեր:

−4≤x≤5 կամ x∈[−4;5]: Կարդում ենք՝ «−4, 5 հատված», կամ «փակ միջակայք»: Նկատենք, որ հատվածի ծայրակետերը ընդգրկված են (սևացված են):

−4≤x<5 կամ x∈[−4;5): Կարդում ենք՝ «−4, 5 կիսաինտերվալ», կամ «կիսաբաց միջակայք»: Նկատենք, որ կիսաինտերվալի ծայրակետերից մեկը՝ −4 -ը ընդգրկված է (սևացված է), իսկ մյուսը՝ 5 -ը ընդգրկված չէ (սևացված չէ):

−4<x≤5 կամ x∈(−4;5]: Սա ևս կիսաինտերվալ է՝ բաց ձախ ծայրակետով:

Առաջադրանքներ․

1)Անվանեք թվային բազմությանը պատկանող բոլոր ամբողջ թվերը՝

ա)[-3;1]

բ)(-3;1)

գ)[-3;1)

դ)(-3;1]

ե)[-2;3]

զ)(-2;3)

է)[-2;3)

ը)(-2;3]

2)Պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա)[3;5]

բ)(3;5)

գ)[3;5)

դ)(3;5]

ե)[-2;+∞)

զ)(-2;+∞)

է)(-∞;-2)

ը)(-∞;-2]

3)Պատկանու՞մ է արդյոք -2 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)[-3;0]

բ)(-2;3)

գ)(-∞;-2]

դ)(-3;+∞)

ե)N

զ)Z

է)Q

ը)R

4)Անվանեք թվային բազմությանը պատկանող երեք ամբողջ թվեր՝

ա)[0;+∞)

բ)(0;+∞)

գ)(-∞;1)

դ)(-∞;1]

5)Գրառեք նշանակումը և պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա)2-ից 4 փակ միջակայքի (հատվածի)

բ)2-ից 4 բաց միջակայքի

գ)2-ից 4 կիսաբաց միջակայքի՝ 4-ը ներառած

դ)2-ից 4 կիսաբաց միջակայքի՝ 2-ը ներառած

ե)5-ից +∞ միջակայքի

զ)5-ից +∞ կիսաբաց միջակայքի

է) -∞-ից 0 միջակայքի

ը) -∞-ից 0 կիսաբաց միջակայքի

6)Պատկանու՞մ է արդյոք 2/3 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)(0;1]

բ)[1;2]

գ)(-∞;2/3]

դ)(2/3;+∞)

ե)N

զ)Z

է)Q

ը)RԳիտենք, որ իրական թվերի երկրաչափական մոդելը թվային ուղիղն է: Ցանկացած իրական թիվ թվային ուղղի վրա ունի իր դիրքը: Հիմա կպարզենք, թե ինչպես են թվային ուղղի վրա պատկերվում թվային միջակայքերը: Կօգտագործենք հետևյալ նշանակումները. 

Անհավասարությունների և ծայրակետերի նշանակումներ	Բազմությունների նշանակումներ
≤ կամ ≥ ∙ (ծայրակետն ընդգրկված է)	[ և]քառակուսի փակագծեր
< կամ > о (ծայրակետն ընդգրկված չէ)	( և )կլոր փակագծեր

Գոյություն ունեն թվային ուղղի վրա բազմությունների 4 տեսակի նշանակումներ:

Ամբողջ թվային ուղիղը նշանակվում է այսպես՝ (−∞;∞)։

Եթե x թիվը միաժամանակ բավարարում է x>−4 և x<5 անհավասարություններին, ապա այն բավարարում է −4<x<5 երկկողմանի անհավասարությանը:

−4<x<5 երկկողմանի անհավասարությանը բավարարող բոլոր թվերի բազմությունը անվանում են թվային միջակայք և նշանակում են այսպես՝ (−4;5):

Միջակայքը պատկերենք թվային ուղղի վրա: Կարդում ենք՝ «−4, 5 ինտերվալ», կամ «բաց միջակայք» : Նկատենք, որ հատվածի ծայրակետերը ընդգրկված չեն (սևացված չեն):

Դիտարկենք ուրիշ միջակայքեր:

−4≤x≤5 կամ x∈[−4;5]: Կարդում ենք՝ «−4, 5 հատված», կամ «փակ միջակայք»: Նկատենք, որ հատվածի ծայրակետերը ընդգրկված են (սևացված են):

−4≤x<5 կամ x∈[−4;5): Կարդում ենք՝ «−4, 5 կիսաինտերվալ», կամ «կիսաբաց միջակայք»: Նկատենք, որ կիսաինտերվալի ծայրակետերից մեկը՝ −4 -ը ընդգրկված է (սևացված է), իսկ մյուսը՝ 5 -ը ընդգրկված չէ (սևացված չէ):

−4<x≤5 կամ x∈(−4;5]: Սա ևս կիսաինտերվալ է՝ բաց ձախ ծայրակետով:

Առաջադրանքներ․

1)Անվանեք թվային բազմությանը պատկանող բոլոր ամբողջ թվերը՝

ա)[-3;1]=

բ)(-3;1)=

գ)[-3;1)=

դ)(-3;1]=

ե)[-2;3]=

զ)(-2;3)=

է)[-2;3)

ը)(-2;3]

2)Պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա)[3;5]-3,4,5

բ)(3;5)-4

գ)[3;5)-34,

դ)(3;5]-4,5

ե)[-2;+∞)-2+

զ)(-2;+∞)

է)(-∞;-2)

ը)(-∞;-2]+2

3)Պատկանու՞մ է արդյոք -2 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)-2∈[-3;0]

բ)-2∈(-2;3)

գ)-2∈(-∞;-2]

դ)-2(-3;+∞)

ե)N

զ)Z

է)Q

ը)R

4)Անվանեք թվային բազմությանը պատկանող երեք ամբողջ թվեր՝

ա)[0;+∞)

բ)(0;+∞)

գ)(-∞;1)

դ)(-∞;1]

5)Գրառեք նշանակումը և պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա)2-ից 4 փակ միջակայքի (հատվածի)

բ)2-ից 4 բաց միջակայքի

գ)2-ից 4 կիսաբաց միջակայքի՝ 4-ը ներառած

դ)2-ից 4 կիսաբաց միջակայքի՝ 2-ը ներառած

ե)5-ից +∞ միջակայքի

զ)5-ից +∞ կիսաբաց միջակայքի

է) -∞-ից 0 միջակայքի

ը) -∞-ից 0 կիսաբաց միջակայքի

6)Պատկանու՞մ է արդյոք 2/3 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)(0;1]

բ)[1;2]

գ)(-∞;2/3]

դ)(2/3;+∞)

ե)N

զ)Z

է)Q

ը)R