Շրջանագծին ներգծված է ABC եռանկյունն այնպես, որ AB-ն տրամագիծ է։ Գտեք եռանկյան անկյունները, եթե՝
ա) U BC=1340
բ)U AC=700
2)Շրջանագծին ներգծված է BC հիմքով ABC հավասարասրուն եռանկյունը։ Գտեք եռանկյան անկյունները, եթե U BC=1020։
3)Ուղղանկյուն եռանկյան ներքնաձիգը 13 սմ է, իսկ էջերի գումարը՝ 17 սմ։ Գտեք եռանկյան ներգծյալ շրջանագծի շառավիղը։
4)Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36 սմ։ Գտեք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը։
5)ABC եռանկյանը արտագծված է շրջանագիծ։ Գտեք այդ շրջանագծի շառավիղը, եթե AC=24սմ, <A=600, <B=300 ։
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:
Շրջանագծի կենտրոնը հավասարահեռ է բազմանկյան բոլոր գագաթներից, հետևաբար այն գտնվում է բազմանկյան կողմերի միջնուղղահայացների հատման կետում:
Ոչ բոլոր բազմանկյուններն ունեն արտագծյալ շրջանագիծ՝ հաճախ բազմանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի բազմանկյան բոլոր գագաթներով:
Քանի որ եռանկյան կողմերի միջնուղղահայացները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի արտագծյալ շրջանագիծ:
Սուրանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներսում (տես ներքևի նկարը):
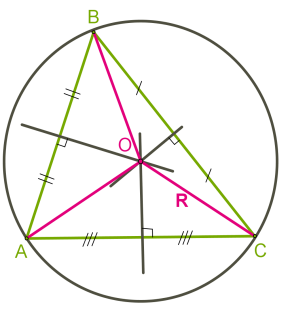
Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի միջնակետում (տես ներքևի նկարը):
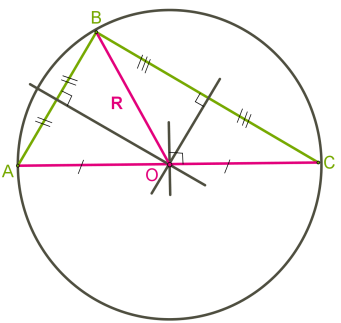
Բութանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյունից դուրս (տես ներքևի նկարը):
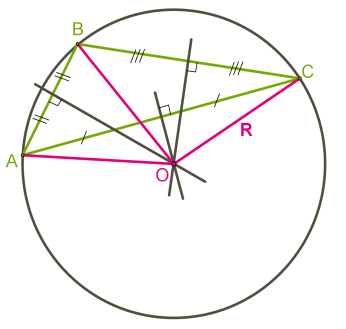
Ներգծյալ շրջանագիծ․
Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:
Ներգծված շրջանագծի կենտրոնը պետք է հավասարահեռ լինի բազմանկյան կողմերից, այսինքն լինի կիսորդների հատման կետում:
Քանի որ եռանկյան անկյունների կիսորդները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի ներգծյալ շրջանագիծ:
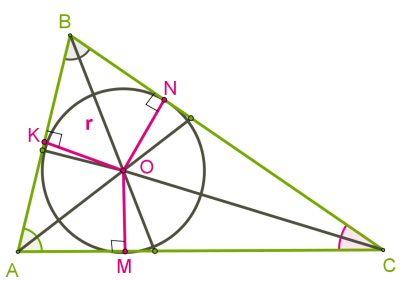
Քանի որ, ցանկացած եռանկյան անկյունների կիսորդները հատվում են եռանկյան ներսում, ապա ներգծյալ շրջանագծի կենտրոնը միշտ գտնվում է եռանկյան ներսում:
Առաջադրանքներ.
1.Նշիր եռանկյունները, որոնց արտագծված է շրջանագիծ:
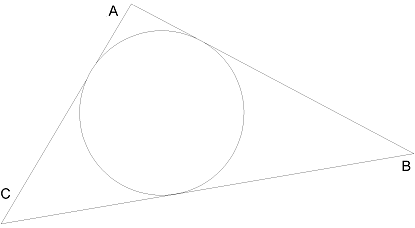
2.Նշիր եռանկյունները, որոնց ներգծված է շրջանագիծ:
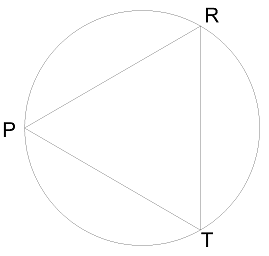
3. Եռանկյանը ներգծված է շրջանագիծ: Հաշվիր <COA, <AOB, <COB եթե ∢OMN=32° և ∢ONL=37°
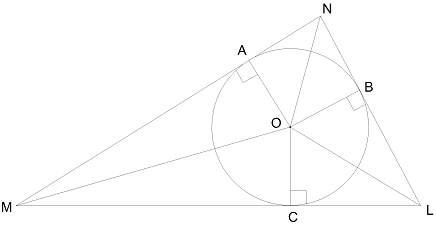
4.Ներգծյալ շրջանագծի շոշափման կետում հավասարասրուն եռանկյան սրունքը տրոհվում է 3սմ և 4սմ երկարությամբ հատվածների՝ հաշված հիմքից։ Գտեք այդ եռանկյան պարագիծը։
5.Գտեք 6 սմ և 8 սմ էջերով և 10 սմ ներքնաձիգով ուղղանկյուն եռանկյանը ներգծած շրջանագծի շառավիղը։
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)Գծագրերում գտնե՛լ ABC անկյունը․





2)Գծագրերում գտնել x աղեղը․


3)Գծագրերում գտնել x անկյունը․


4)Գտնել անհայտ անկյունները․

Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Ըստ գծագրերի տվյալների գտեք անհայտ անկյունը․
1)

2)

3)

4)

5)

6)

7)A, B, C և D կետերը գտնվում են շրջանագծի վրա։Ապացուցեք, որ եթե աղեղ AB = CD, ապա AB = CD:
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)O կենտրոնով շրջանագծի AB աղեղը 90o է։ Գտեք O կետի հեռավորությունը AB լարից, եթե AB = 24 սմ։
2)O կենտրոնով շրջանագծի AB աղեղը 120o է։ Գտեք O կետի հեռավորությունը AB լարից, եթե շրջանագծի շառավիղը 20 սմ է։
3)AB — ն և AC — ն շրջանագծի լարեր են։ <BAC = 70o , աղեղ AB = 120o ։ Գտեք AC աղեղի աստիճանային չափը։
4)Շրջանագծում տարված են AB տրամագիծը և AC լարը։ Գտեք BAC անկյունը, եթե կիսաշրջանագիծը C կետով տրոհվում է AC և CB աղեղների, որոնց աստիճանային չափերը հարաբերում են, ինչպես 7 : 2 :
5)AB — ն շրջանագծի տրամագիծն է։ Շրջանագծի վրա վերցված է C կետն այնպես, որ BC լարը հավասար է շրջանագծի շառավիղին։ Գտեք ABC եռանկյան անկյունները։
Ներգծյալ և կենտրոնային անկյուն
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)Ըստ գծագրերի տվյալների՝ գտեք x-ը․
ա)

բ)

գ)

դ)

2)AB կիսաշրջանագծի վրա վերցված են C և D կետերն այնպես, որ
∪AC=57o, ∪BD=63o
Գտեք CD լարը, եթե շրջանագծի շառավիղը 12 սմ է։
3)AOB կենտրոնային անկյունը 30o -ով մեծ է AB աղեղին հենված ներգծյալ անկյունից։ Գտեք այդ անկյուններից յուրաքանչյուրը։
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Շրջանագծի ցանկացած երկու կետեր շրջանագիծը տրոհում են երկու մասի, որոնցից յուրաքանչյուրը կոչվում է շրջանագծի աղեղ:
Եթե շրջանագծի վրա նշենք երկու կետ, ապա առաջանում են երկու աղեղներ: Այդ պատճառով աղեղի նշանակման համար օգտագործում են լատիներեն երեք տառ, որոնք կարող են լինել ինչպես մեծատառեր, այնպես էլ՝ փոքրատառեր:
Վերևի նկարում կարող ենք նշել BDH, ACG և մյուս աղեղները:
Ներքևի նկարում գծված են AxB և AyB աղեղները:
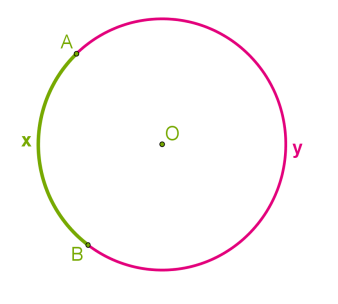
Աղեղը կոչվում է կիսաշրջանագիծ, եթե նրա ծայրերը միացնող հատվածը այդ շրջանագծի տրամագիծ է:
Կենտրոնային անկյուն․
Անկյունը, որի գագաթը շրջանի կենտրոնն է, կոչվում է նրա կենտրոնային անկյուն:

Դիցուք O կենտրոնով շրջանի կենտրոնային անկյան կողմերը շրջանագիծը հատում են A և B կետերում: AOB կենտրոնային անկյանը համապատասխանում են A և B ծայրերով երկու աղեղ: Եթե <AOB-ն փռված է, ապա նրան համապատասխանում է երկու կիսաշրջանագիծ: Իսկ եթե անկյունը փռված չէ, ապա ասում են, որ այդ անկյան ներսում ընկած աղեղը փոքր է կիսաշրջանագծից, մյուսը՝ մեծ:
Շրջանագծի աղեղը կարելի է չափել աստիճաններով:
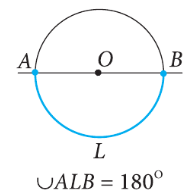
Եթե O կենտրոնով շրջանագծի AB աղեղը փոքր է կիսաշրջանագծից կամ կիսաշրջանագիծ է, ապա համարվում է, որ նրա աստիճանային չափը հավասար է AOB կենտրոնային անկյան աստիճանային չափին:
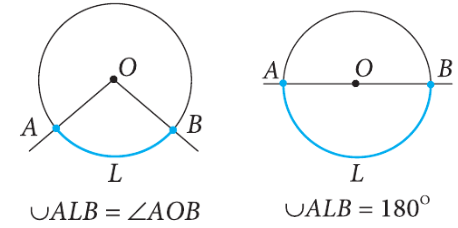
Իսկ եթե AB աղեղը մեծ է կիսաշրջանագծից, ապա համարվում է, որ նրա աստիճանային չափը հավասար է 3600 — <AOB:
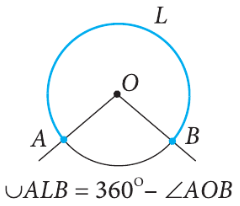
Այստեղից հետևում է, որ շրջանագծի՝ ընդհանուր ծայրեր ունեցող երկու աղեղների աստիճանային չափերի գումարը հավասար է 3600:
Ներգծյալ անկյուն․
Այն անկյունը, որի գագաթն ընկած է շրջանագծի վրա, իսկ կողմերը շրջանագիծը հատում են, կոչվում է ներգծյալ անկյուն:
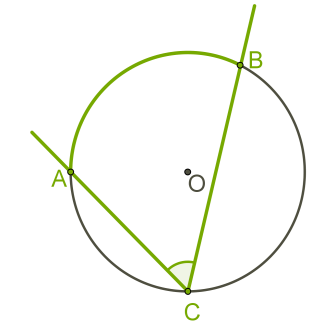
Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա նա հենվում է՝
∡ACB=1/2∪AB
1. Նույն աղեղի վրա հենված ներգծյալ անկյունները հավասար են:
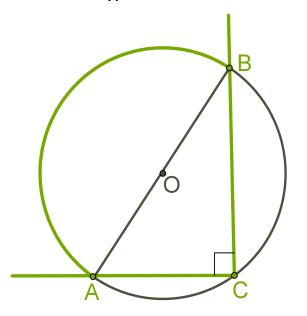
2. Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է:
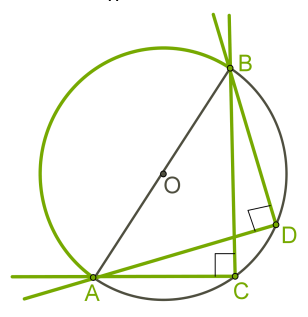
Առաջադրանքներ․
1.Որքա՞ն է ներգծյալ անկյունը, որը հենված է 28° աստիճանային չափով աղեղի վրա:
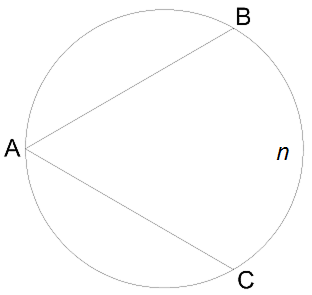
2.Դիցուք BAC անկյունը 35° է: Որքա՞ն է BnC աղեղի աստիճանային չափը։
3.Գտիր ASB անկյունը, եթե ASB աղեղի աստիճանային չափը 268° է:

4.Գտիր BOC և BAC անկյունները, եթե ∪AB=130° ∪AC=150° ։
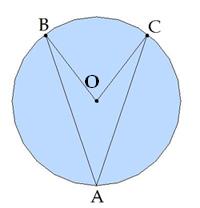
5.Հաշվիր AOB եռանկյան անկյունները, եթե ∪AB=100°։
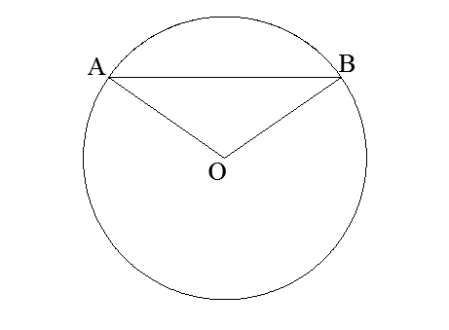
6. ACB աղեղի աստիճանային չափը 260° է: Գտիր AOB և ACB անկյունները:

Պատկերացում կոնի մասին
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Կոնը կարելի է ստանալ՝ պտտելով POA ուղղանկյուն եռանկյունը իր էջերից որևէ մեկի, օրինակ՝ PO-ի շուրջ: Նույն կոնը կստացվի, եթե APB հավասարասրուն եռանկյունը պտտենք PO բարձրության շուրջ:
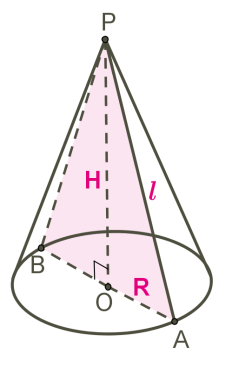
PO ուղիղը կոչվում է կոնի առանցք, որը պարունակում է կոնի H բարձրությունը:
Կոնի առանցքային հատույթը, որը անցնում է նրա գագաթով, հանդիսանում է PA և PB սրունքներով հավասարասրուն եռանկյուն: PA-ն և PB-ն կոչվում են կոնի ծնորդներ և նշանակվում են l տառով:
Եռանկյան պտույտից առաջացած O կենտրոնով շրջանը կոչվում է կոնի հիմք:
Կոնի շառավիղ կոչվում է նրա հիմքի R=OA=OB շառավիղը:
Առաջադրանքներ․
1)30o անկյուն ունեցող ուղղանկյուն եռանկյունը պտտվում է մեծ էջի շուրջը։ Գտեք պտտումից առաջացած կոնի ծնորդը, եթե այդ կոնի շառավիղը 15 սմ է:
2)Կոնի առանցքային հատույթը 12 սմ կողմով հավասարակողմ եռանկյուն է։ Որոշեք այդ կոնի շառավիղն ու ծնորդը։
3)Կոնի առանցքային հատույթը հավասարասրուն ուղղանկյուն եռանկյուն է, որի ներքնաձիգը 20 սմ է։ Գտեք այդ կոնի շառավիղը։
Պատկերացում գլանի մասին
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Գլան կարելի է ստանալ՝ պտտելով AA1O1O ուղղանկյունը իր կողմերից որևէ մեկի, օրինակ՝ OO1-ի շուրջ: Նույն գլանը կարելի է ստանալ՝ պտտելով AA1B1B ուղղանկյունն իր հանդիպակաց կողմերի միջնակետերով անցնող OO1 ուղղի շուրջ:
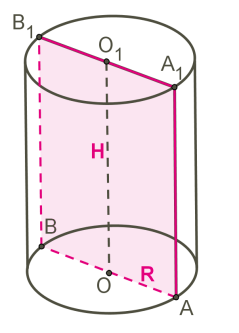
OO1 ուղիղը կոչվում է գլանի առանցք, AA1-ը և BB1-ը՝ ծնորդներ: Գլանի H բարձրությունը հավասար է OO1=AA1=BB1 հատվածներից յուրաքանչյուրին:
Պտտման ընթացքում առաջացած երկու շրջանները կոչվում են գլանի հիմքեր:
Գլանի R=OA=OB շառավիղ կոչվում է նրա հիմքի շառավիղը:
Գլանի առանցքով անցնող հարթության և գլանի ընդհանուր մասը կոչվում է գլանի առանցքային հատույթ: Գլանի առանցքային հատույթը ուղղանկյուն է: Վերևի նկարում դա AA1B1B ուղղանկյունն է:
Առաջադրանքներ․
1)Գլանաձև բաժակը կիսով չափ լցված է թեյով։Գոլորշիանալուց հետո թեյի հետքը մնացել էր բաժակի պատերին։ Երկրաչափական ի՞նչ պատկեր է այդ հետքը։
2)Գլանի առանցքային հատույթը քառակուսի է։ Գտեք գլանի ծնորդի և շառավիղի երկարությունների հարաբերությունը։
3)Գլանի առանցքային հատույթը 40 սմ պարագծով մի ուղղանկյուն է, որի անկյունագծերը փոխուղղահայաց են։ Գտեք գլանի շառավիղը։
4)Գլանի առանցքային հատույթը մի ուղղանկյուն է, որի անկյունագիծը ծնորդ հանդիսացող կողմի հետ կազմում է 60o -ի անկյուն։ Գտեք այդ անկյունագիծը, եթե գլանի ծնորդի երկարությունը 6 սմ է։
Շրջանագիծ
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Շրջանագծին ներգծված է ABC եռանկյունն այնպես, որ AB-ն տրամագիծ է։ Գտեք եռանկյան անկյունները, եթե՝
ա) U BC=1340
բ)U AC=700
2)Շրջանագծին ներգծված է BC հիմքով ABC հավասարասրուն եռանկյունը։ Գտեք եռանկյան անկյունները, եթե U BC=1020։
3)Ուղղանկյուն եռանկյան ներքնաձիգը 13 սմ է, իսկ էջերի գումարը՝ 17 սմ։ Գտեք եռանկյան ներգծյալ շրջանագծի շառավիղը։
4)Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36 սմ։ Գտեք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը։
5)ABC եռանկյանը արտագծված է շրջանագիծ։ Գտեք այդ շրջանագծի շառավիղը, եթե AC=24սմ, <A=600, <B=300 ։
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:
Շրջանագծի կենտրոնը հավասարահեռ է բազմանկյան բոլոր գագաթներից, հետևաբար այն գտնվում է բազմանկյան կողմերի միջնուղղահայացների հատման կետում:
Ոչ բոլոր բազմանկյուններն ունեն արտագծյալ շրջանագիծ՝ հաճախ բազմանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի բազմանկյան բոլոր գագաթներով:
Քանի որ եռանկյան կողմերի միջնուղղահայացները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի արտագծյալ շրջանագիծ:
Սուրանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներսում (տես ներքևի նկարը):

Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի միջնակետում (տես ներքևի նկարը):

Բութանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյունից դուրս (տես ներքևի նկարը):

Ներգծյալ շրջանագիծ․
Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:
Ներգծված շրջանագծի կենտրոնը պետք է հավասարահեռ լինի բազմանկյան կողմերից, այսինքն լինի կիսորդների հատման կետում:
Քանի որ եռանկյան անկյունների կիսորդները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի ներգծյալ շրջանագիծ:

Քանի որ, ցանկացած եռանկյան անկյունների կիսորդները հատվում են եռանկյան ներսում, ապա ներգծյալ շրջանագծի կենտրոնը միշտ գտնվում է եռանկյան ներսում:
Առաջադրանքներ.
1.Նշիր եռանկյունները, որոնց արտագծված է շրջանագիծ:

2.Նշիր եռանկյունները, որոնց ներգծված է շրջանագիծ:

3. Եռանկյանը ներգծված է շրջանագիծ: Հաշվիր <COA, <AOB, <COB եթե ∢OMN=32° և ∢ONL=37°

4.Ներգծյալ շրջանագծի շոշափման կետում հավասարասրուն եռանկյան սրունքը տրոհվում է 3սմ և 4սմ երկարությամբ հատվածների՝ հաշված հիմքից։ Գտեք այդ եռանկյան պարագիծը։
5.Գտեք 6 սմ և 8 սմ էջերով և 10 սմ ներքնաձիգով ուղղանկյուն եռանկյանը ներգծած շրջանագծի շառավիղը։
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)Գծագրերում գտնե՛լ ABC անկյունը․





2)Գծագրերում գտնել x աղեղը․


3)Գծագրերում գտնել x անկյունը․


4)Գտնել անհայտ անկյունները․

Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Ըստ գծագրերի տվյալների գտեք անհայտ անկյունը․
1)

2)

3)

4)

5)

6)

7)A, B, C և D կետերը գտնվում են շրջանագծի վրա։Ապացուցեք, որ եթե աղեղ AB = CD, ապա AB = CD:
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)O կենտրոնով շրջանագծի AB աղեղը 90o է։ Գտեք O կետի հեռավորությունը AB լարից, եթե AB = 24 սմ։
2)O կենտրոնով շրջանագծի AB աղեղը 120o է։ Գտեք O կետի հեռավորությունը AB լարից, եթե շրջանագծի շառավիղը 20 սմ է։
3)AB — ն և AC — ն շրջանագծի լարեր են։ <BAC = 70o , աղեղ AB = 120o ։ Գտեք AC աղեղի աստիճանային չափը։
4)Շրջանագծում տարված են AB տրամագիծը և AC լարը։ Գտեք BAC անկյունը, եթե կիսաշրջանագիծը C կետով տրոհվում է AC և CB աղեղների, որոնց աստիճանային չափերը հարաբերում են, ինչպես 7 : 2 :
5)AB — ն շրջանագծի տրամագիծն է։ Շրջանագծի վրա վերցված է C կետն այնպես, որ BC լարը հավասար է շրջանագծի շառավիղին։ Գտեք ABC եռանկյան անկյունները։
Ներգծյալ և կենտրոնային անկյուն
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)Ըստ գծագրերի տվյալների՝ գտեք x-ը․
ա)

բ)

գ)

դ)

2)AB կիսաշրջանագծի վրա վերցված են C և D կետերն այնպես, որ
∪AC=57o, ∪BD=63o
Գտեք CD լարը, եթե շրջանագծի շառավիղը 12 սմ է։
3)AOB կենտրոնային անկյունը 30o -ով մեծ է AB աղեղին հենված ներգծյալ անկյունից։ Գտեք այդ անկյուններից յուրաքանչյուրը։
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Շրջանագծի ցանկացած երկու կետեր շրջանագիծը տրոհում են երկու մասի, որոնցից յուրաքանչյուրը կոչվում է շրջանագծի աղեղ:
Եթե շրջանագծի վրա նշենք երկու կետ, ապա առաջանում են երկու աղեղներ: Այդ պատճառով աղեղի նշանակման համար օգտագործում են լատիներեն երեք տառ, որոնք կարող են լինել ինչպես մեծատառեր, այնպես էլ՝ փոքրատառեր:
Վերևի նկարում կարող ենք նշել BDH, ACG և մյուս աղեղները:
Ներքևի նկարում գծված են AxB և AyB աղեղները:

Աղեղը կոչվում է կիսաշրջանագիծ, եթե նրա ծայրերը միացնող հատվածը այդ շրջանագծի տրամագիծ է:

Կենտրոնային անկյուն․
Անկյունը, որի գագաթը շրջանի կենտրոնն է, կոչվում է նրա կենտրոնային անկյուն:

Դիցուք O կենտրոնով շրջանի կենտրոնային անկյան կողմերը շրջանագիծը հատում են A և B կետերում: AOB կենտրոնային անկյանը համապատասխանում են A և B ծայրերով երկու աղեղ: Եթե <AOB-ն փռված է, ապա նրան համապատասխանում է երկու կիսաշրջանագիծ: Իսկ եթե անկյունը փռված չէ, ապա ասում են, որ այդ անկյան ներսում ընկած աղեղը փոքր է կիսաշրջանագծից, մյուսը՝ մեծ:
Շրջանագծի աղեղը կարելի է չափել աստիճաններով:
Եթե O կենտրոնով շրջանագծի AB աղեղը փոքր է կիսաշրջանագծից կամ կիսաշրջանագիծ է, ապա համարվում է, որ նրա աստիճանային չափը հավասար է AOB կենտրոնային անկյան աստիճանային չափին:

Իսկ եթե AB աղեղը մեծ է կիսաշրջանագծից, ապա համարվում է, որ նրա աստիճանային չափը հավասար է 3600 — <AOB:

Այստեղից հետևում է, որ շրջանագծի՝ ընդհանուր ծայրեր ունեցող երկու աղեղների աստիճանային չափերի գումարը հավասար է 3600:
Ներգծյալ անկյուն․
Այն անկյունը, որի գագաթն ընկած է շրջանագծի վրա, իսկ կողմերը շրջանագիծը հատում են, կոչվում է ներգծյալ անկյուն:

Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա նա հենվում է՝
∡ACB=1/2∪AB
1. Նույն աղեղի վրա հենված ներգծյալ անկյունները հավասար են:
2. Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է:


Առաջադրանքներ․
1.Որքա՞ն է ներգծյալ անկյունը, որը հենված է 28° աստիճանային չափով աղեղի վրա:
2.Դիցուք BAC անկյունը 35° է: Որքա՞ն է BnC աղեղի աստիճանային չափը։

3.Գտիր ASB անկյունը, եթե ASB աղեղի աստիճանային չափը 268° է:

4.Գտիր BOC և BAC անկյունները, եթե ∪AB=130° ∪AC=150° ։

5.Հաշվիր AOB եռանկյան անկյունները, եթե ∪AB=100°։

6. ACB աղեղի աստիճանային չափը 260° է: Գտիր AOB և ACB անկյունները:

Պատկերացում կոնի մասին
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Կոնը կարելի է ստանալ՝ պտտելով POA ուղղանկյուն եռանկյունը իր էջերից որևէ մեկի, օրինակ՝ PO-ի շուրջ: Նույն կոնը կստացվի, եթե APB հավասարասրուն եռանկյունը պտտենք PO բարձրության շուրջ:

PO ուղիղը կոչվում է կոնի առանցք, որը պարունակում է կոնի H բարձրությունը:
Կոնի առանցքային հատույթը, որը անցնում է նրա գագաթով, հանդիսանում է PA և PB սրունքներով հավասարասրուն եռանկյուն: PA-ն և PB-ն կոչվում են կոնի ծնորդներ և նշանակվում են l տառով:
Եռանկյան պտույտից առաջացած O կենտրոնով շրջանը կոչվում է կոնի հիմք:
Կոնի շառավիղ կոչվում է նրա հիմքի R=OA=OB շառավիղը:
Առաջադրանքներ․
1)30o անկյուն ունեցող ուղղանկյուն եռանկյունը պտտվում է մեծ էջի շուրջը։ Գտեք պտտումից առաջացած կոնի ծնորդը, եթե այդ կոնի շառավիղը 15 սմ է:
2)Կոնի առանցքային հատույթը 12 սմ կողմով հավասարակողմ եռանկյուն է։ Որոշեք այդ կոնի շառավիղն ու ծնորդը։
3)Կոնի առանցքային հատույթը հավասարասրուն ուղղանկյուն եռանկյուն է, որի ներքնաձիգը 20 սմ է։ Գտեք այդ կոնի շառավիղը։
Պատկերացում գլանի մասին
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Գլան կարելի է ստանալ՝ պտտելով AA1O1O ուղղանկյունը իր կողմերից որևէ մեկի, օրինակ՝ OO1-ի շուրջ: Նույն գլանը կարելի է ստանալ՝ պտտելով AA1B1B ուղղանկյունն իր հանդիպակաց կողմերի միջնակետերով անցնող OO1 ուղղի շուրջ:

OO1 ուղիղը կոչվում է գլանի առանցք, AA1-ը և BB1-ը՝ ծնորդներ: Գլանի H բարձրությունը հավասար է OO1=AA1=BB1 հատվածներից յուրաքանչյուրին:
Պտտման ընթացքում առաջացած երկու շրջանները կոչվում են գլանի հիմքեր:
Գլանի R=OA=OB շառավիղ կոչվում է նրա հիմքի շառավիղը:
Գլանի առանցքով անցնող հարթության և գլանի ընդհանուր մասը կոչվում է գլանի առանցքային հատույթ: Գլանի առանցքային հատույթը ուղղանկյուն է: Վերևի նկարում դա AA1B1B ուղղանկյունն է:
Առաջադրանքներ․
1)Գլանաձև բաժակը կիսով չափ լցված է թեյով։Գոլորշիանալուց հետո թեյի հետքը մնացել էր բաժակի պատերին։ Երկրաչափական ի՞նչ պատկեր է այդ հետքը։
2)Գլանի առանցքային հատույթը քառակուսի է։ Գտեք գլանի ծնորդի և շառավիղի երկարությունների հարաբերությունը։
3)Գլանի առանցքային հատույթը 40 սմ պարագծով մի ուղղանկյուն է, որի անկյունագծերը փոխուղղահայաց են։ Գտեք գլանի շառավիղը։
4)Գլանի առանցքային հատույթը մի ուղղանկյուն է, որի անկյունագիծը ծնորդ հանդիսացող կողմի հետ կազմում է 60o -ի անկյուն։ Գտեք այդ անկյունագիծը, եթե գլանի ծնորդի երկարությունը 6 սմ է։
Շրջանագիծ
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1Շրջանագծին ներգծված է ABC եռանկյունն այնպես, որ AB-ն տրամագիծ է։ Գտեք եռանկյան անկյունները, եթե՝
ա) U BC=1340
բ)U AC=700
2)Շրջանագծին ներգծված է BC հիմքով ABC հավասարասրուն եռանկյունը։ Գտեք եռանկյան անկյունները, եթե U BC=1020։
3)Ուղղանկյուն եռանկյան ներքնաձիգը 13 սմ է, իսկ էջերի գումարը՝ 17 սմ։ Գտեք եռանկյան ներգծյալ շրջանագծի շառավիղը։
4)Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36 սմ։ Գտեք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը։
5)ABC եռանկյանը արտագծված է շրջանագիծ։ Գտեք այդ շրջանագծի շառավիղը, եթե AC=24սմ, <A=600, <B=300 ։
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:
Շրջանագծի կենտրոնը հավասարահեռ է բազմանկյան բոլոր գագաթներից, հետևաբար այն գտնվում է բազմանկյան կողմերի միջնուղղահայացների հատման կետում:
Ոչ բոլոր բազմանկյուններն ունեն արտագծյալ շրջանագիծ՝ հաճախ բազմանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի բազմանկյան բոլոր գագաթներով:
Քանի որ եռանկյան կողմերի միջնուղղահայացները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի արտագծյալ շրջանագիծ:
Սուրանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներսում (տես ներքևի նկարը):

Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի միջնակետում (տես ներքևի նկարը):

Բութանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյունից դուրս (տես ներքևի նկարը):

Ներգծյալ շրջանագիծ․
Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:
Ներգծված շրջանագծի կենտրոնը պետք է հավասարահեռ լինի բազմանկյան կողմերից, այսինքն լինի կիսորդների հատման կետում:
Քանի որ եռանկյան անկյունների կիսորդները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի ներգծյալ շրջանագիծ:

Քանի որ, ցանկացած եռանկյան անկյունների կիսորդները հատվում են եռանկյան ներսում, ապա ներգծյալ շրջանագծի կենտրոնը միշտ գտնվում է եռանկյան ներսում:
Առաջադրանքներ.
1.Նշիր եռանկյունները, որոնց արտագծված է շրջանագիծ:

2.Նշիր եռանկյունները, որոնց ներգծված է շրջանագիծ:

3. Եռանկյանը ներգծված է շրջանագիծ: Հաշվիր <COA, <AOB, <COB եթե ∢OMN=32° և ∢ONL=37°

4.Ներգծյալ շրջանագծի շոշափման կետում հավասարասրուն եռանկյան սրունքը տրոհվում է 3սմ և 4սմ երկարությամբ հատվածների՝ հաշված հիմքից։ Գտեք այդ եռանկյան պարագիծը։
5.Գտեք 6 սմ և 8 սմ էջերով և 10 սմ ներքնաձիգով ուղղանկյուն եռանկյանը ներգծած շրջանագծի շառավիղը։
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)Գծագրերում գտնե՛լ ABC անկյունը․





2)Գծագրերում գտնել x աղեղը․


3)Գծագրերում գտնել x անկյունը․


4)Գտնել անհայտ անկյունները․

Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Ըստ գծագրերի տվյալների գտեք անհայտ անկյունը․
1)

2)

3)

4)

5)

6)

7)A, B, C և D կետերը գտնվում են շրջանագծի վրա։Ապացուցեք, որ եթե աղեղ AB = CD, ապա AB = CD:
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)O կենտրոնով շրջանագծի AB աղեղը 90o է։ Գտեք O կետի հեռավորությունը AB լարից, եթե AB = 24 սմ։
2)O կենտրոնով շրջանագծի AB աղեղը 120o է։ Գտեք O կետի հեռավորությունը AB լարից, եթե շրջանագծի շառավիղը 20 սմ է։
3)AB — ն և AC — ն շրջանագծի լարեր են։ <BAC = 70o , աղեղ AB = 120o ։ Գտեք AC աղեղի աստիճանային չափը։
4)Շրջանագծում տարված են AB տրամագիծը և AC լարը։ Գտեք BAC անկյունը, եթե կիսաշրջանագիծը C կետով տրոհվում է AC և CB աղեղների, որոնց աստիճանային չափերը հարաբերում են, ինչպես 7 : 2 :
5)AB — ն շրջանագծի տրամագիծն է։ Շրջանագծի վրա վերցված է C կետն այնպես, որ BC լարը հավասար է շրջանագծի շառավիղին։ Գտեք ABC եռանկյան անկյունները։
Ներգծյալ և կենտրոնային անկյուն
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
1)Ըստ գծագրերի տվյալների՝ գտեք x-ը․
ա)

բ)

գ)

դ)

2)AB կիսաշրջանագծի վրա վերցված են C և D կետերն այնպես, որ
∪AC=57o, ∪BD=63o
Գտեք CD լարը, եթե շրջանագծի շառավիղը 12 սմ է։
3)AOB կենտրոնային անկյունը 30o -ով մեծ է AB աղեղին հենված ներգծյալ անկյունից։ Գտեք այդ անկյուններից յուրաքանչյուրը։
Շրջանագծի աղեղի աստիճանային չափը
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Շրջանագծի ցանկացած երկու կետեր շրջանագիծը տրոհում են երկու մասի, որոնցից յուրաքանչյուրը կոչվում է շրջանագծի աղեղ:
Եթե շրջանագծի վրա նշենք երկու կետ, ապա առաջանում են երկու աղեղներ: Այդ պատճառով աղեղի նշանակման համար օգտագործում են լատիներեն երեք տառ, որոնք կարող են լինել ինչպես մեծատառեր, այնպես էլ՝ փոքրատառեր:
Վերևի նկարում կարող ենք նշել BDH, ACG և մյուս աղեղները:
Ներքևի նկարում գծված են AxB և AyB աղեղները:

Աղեղը կոչվում է կիսաշրջանագիծ, եթե նրա ծայրերը միացնող հատվածը այդ շրջանագծի տրամագիծ է:

Կենտրոնային անկյուն․
Անկյունը, որի գագաթը շրջանի կենտրոնն է, կոչվում է նրա կենտրոնային անկյուն:

Դիցուք O կենտրոնով շրջանի կենտրոնային անկյան կողմերը շրջանագիծը հատում են A և B կետերում: AOB կենտրոնային անկյանը համապատասխանում են A և B ծայրերով երկու աղեղ: Եթե <AOB-ն փռված է, ապա նրան համապատասխանում է երկու կիսաշրջանագիծ: Իսկ եթե անկյունը փռված չէ, ապա ասում են, որ այդ անկյան ներսում ընկած աղեղը փոքր է կիսաշրջանագծից, մյուսը՝ մեծ:
Շրջանագծի աղեղը կարելի է չափել աստիճաններով:
Եթե O կենտրոնով շրջանագծի AB աղեղը փոքր է կիսաշրջանագծից կամ կիսաշրջանագիծ է, ապա համարվում է, որ նրա աստիճանային չափը հավասար է AOB կենտրոնային անկյան աստիճանային չափին:

Իսկ եթե AB աղեղը մեծ է կիսաշրջանագծից, ապա համարվում է, որ նրա աստիճանային չափը հավասար է 3600 — <AOB:

Այստեղից հետևում է, որ շրջանագծի՝ ընդհանուր ծայրեր ունեցող երկու աղեղների աստիճանային չափերի գումարը հավասար է 3600:
Ներգծյալ անկյուն․
Այն անկյունը, որի գագաթն ընկած է շրջանագծի վրա, իսկ կողմերը շրջանագիծը հատում են, կոչվում է ներգծյալ անկյուն:

Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա նա հենվում է՝
∡ACB=1/2∪AB
1. Նույն աղեղի վրա հենված ներգծյալ անկյունները հավասար են:
2. Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է:


Առաջադրանքներ․
1.Որքա՞ն է ներգծյալ անկյունը, որը հենված է 28° աստիճանային չափով աղեղի վրա:
2.Դիցուք BAC անկյունը 35° է: Որքա՞ն է BnC աղեղի աստիճանային չափը։

3.Գտիր ASB անկյունը, եթե ASB աղեղի աստիճանային չափը 268° է:

4.Գտիր BOC և BAC անկյունները, եթե ∪AB=130° ∪AC=150° ։

5.Հաշվիր AOB եռանկյան անկյունները, եթե ∪AB=100°։

6. ACB աղեղի աստիճանային չափը 260° է: Գտիր AOB և ACB անկյունները:

Պատկերացում կոնի մասին
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Կոնը կարելի է ստանալ՝ պտտելով POA ուղղանկյուն եռանկյունը իր էջերից որևէ մեկի, օրինակ՝ PO-ի շուրջ: Նույն կոնը կստացվի, եթե APB հավասարասրուն եռանկյունը պտտենք PO բարձրության շուրջ:

PO ուղիղը կոչվում է կոնի առանցք, որը պարունակում է կոնի H բարձրությունը:
Կոնի առանցքային հատույթը, որը անցնում է նրա գագաթով, հանդիսանում է PA և PB սրունքներով հավասարասրուն եռանկյուն: PA-ն և PB-ն կոչվում են կոնի ծնորդներ և նշանակվում են l տառով:
Եռանկյան պտույտից առաջացած O կենտրոնով շրջանը կոչվում է կոնի հիմք:
Կոնի շառավիղ կոչվում է նրա հիմքի R=OA=OB շառավիղը:
Առաջադրանքներ․
1)30o անկյուն ունեցող ուղղանկյուն եռանկյունը պտտվում է մեծ էջի շուրջը։ Գտեք պտտումից առաջացած կոնի ծնորդը, եթե այդ կոնի շառավիղը 15 սմ է:
2)Կոնի առանցքային հատույթը 12 սմ կողմով հավասարակողմ եռանկյուն է։ Որոշեք այդ կոնի շառավիղն ու ծնորդը։
3)Կոնի առանցքային հատույթը հավասարասրուն ուղղանկյուն եռանկյուն է, որի ներքնաձիգը 20 սմ է։ Գտեք այդ կոնի շառավիղը։
Պատկերացում գլանի մասին
Երկրաչափություն 8-3, Երկրաչափություն 8-4, Երկրաչափություն 8-9
Գլան կարելի է ստանալ՝ պտտելով AA1O1O ուղղանկյունը իր կողմերից որևէ մեկի, օրինակ՝ OO1-ի շուրջ: Նույն գլանը կարելի է ստանալ՝ պտտելով AA1B1B ուղղանկյունն իր հանդիպակաց կողմերի միջնակետերով անցնող OO1 ուղղի շուրջ:

OO1 ուղիղը կոչվում է գլանի առանցք, AA1-ը և BB1-ը՝ ծնորդներ: Գլանի H բարձրությունը հավասար է OO1=AA1=BB1 հատվածներից յուրաքանչյուրին:
Պտտման ընթացքում առաջացած երկու շրջանները կոչվում են գլանի հիմքեր:
Գլանի R=OA=OB շառավիղ կոչվում է նրա հիմքի շառավիղը:
Գլանի առանցքով անցնող հարթության և գլանի ընդհանուր մասը կոչվում է գլանի առանցքային հատույթ: Գլանի առանցքային հատույթը ուղղանկյուն է: Վերևի նկարում դա AA1B1B ուղղանկյունն է:
Առաջադրանքներ․
1)Գլանաձև բաժակը կիսով չափ լցված է թեյով։Գոլորշիանալուց հետո թեյի հետքը մնացել էր բաժակի պատերին։ Երկրաչափական ի՞նչ պատկեր է այդ հետքը։
2)Գլանի առանցքային հատույթը քառակուսի է։ Գտեք գլանի ծնորդի և շառավիղի երկարությունների հարաբերությունը։
3)Գլանի առանցքային հատույթը 40 սմ պարագծով մի ուղղանկյուն է, որի անկյունագծերը փոխուղղահայաց են։ Գտեք գլանի շառավիղը։
4)Գլանի առանցքային հատույթը մի ուղղանկյուն է, որի անկյունագիծը ծնորդ հանդիսացող կողմի հետ կազմում է 60o -ի անկյուն։ Գտեք այդ անկյունագիծը, եթե գլանի ծնորդի երկարությունը 6 սմ է։
1)Շրջանագծին ներգծված է ABC եռանկյունն այնպես, որ AB-ն տրամագիծ է։ Գտեք եռանկյան անկյունները, եթե՝
ա) U BC=1340
բ)U AC=700
ա․180-67=113
բ․
2)Շրջանագծին ներգծված է BC հիմքով ABC հավասարասրուն եռանկյունը։ Գտեք եռանկյան անկյունները, եթե U BC=1020։
3)Ուղղանկյուն եռանկյան ներքնաձիգը 13 սմ է, իսկ էջերի գումարը՝ 17 սմ։ Գտեք եռանկյան ներգծյալ շրջանագծի շառավիղը։
4)Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36 սմ։ Գտեք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը։