հանրահաշիվ

2x − 6 տառային արտահայտությունն ունի երկու նշանապահպանման միջակայք՝ (−∞,3) և (3,+∞)։ Այդ միջակայքերից առաջինում արտահայտությունը բացասական է, երկրորդում՝դրական։ Դա տեսանելի է նաև y = 2x − 6 ֆունկցիայի գրաֆիկից։

Ինչպես տեսնում ենք, x < 3 դեպքում ֆունկցիայի արժեքը բացասական է (գրաֆիկը x-երի առանցքից ներքև է), իսկ x > 3 դեպքում՝ դրական (գրաֆիկը x-երի առանցքից վերև է): Այն աբսցիսների առանցքը հատում է (3,0) կետում։ Գրաֆիկից երևում է, որ 3-ից ձախ կետերում ֆունկցիայի արժեքները բացասական են, իսկ 3-ից աջ կետերում՝ դրական։ (−∞,3) և (3,+∞) միջակայքերն անվանենք y = 2x − 6 ֆունկցիայի նշանապահպանման միջակայքեր։ Ֆունկցիայի գրաֆիկից հնարավոր է պարզել ֆունկցիայի նշանապահպանման միջակայքերը։
Օրինակ 1․
Պարզենք նկարում պատկերված ֆունկցիայի նշանապահպանման միջակայքերը։

Լուծում․
Գրաֆիկը աբսցիսների (x-երի) առանցքից ներքև է, երբ x-ը փոքր է −4-ից, կամ էլ գտնվում է 1-ի և 3-ի միջև։ Այդ միջակայքերում ֆունկցիայի արժեքները բացասական են։ (−∞, −4) և (1, 3) միջակայքերում ֆունկցիան բացասական է։ Նույն տրամաբանությամբ (−4, 1) և (3, +∞) միջակայքերում ֆունկցիան դրական է։ Վերջում,
նշենք, որ −4, 1 և 3 կետերում ֆունկցիայի արժեքը 0 է։

Իմանալով ֆունկցիայի դրական ու բացասական լինելու միջակայքերը՝ կարող ենք մոտավոր պատկերացում կազմել նրա գրաֆիկի մասին։

Օրինակ 2․
Գծենք ֆունկցիա, որն ունի երեք նշանապահպանման միջակայք՝ (−∞, 3)-ում՝ դրական, իսկ (3, 5)-ում և (5, +∞)-ում՝ բացասական։
Լուծում․
Գծապատկերում պահանջին բավարարող ֆունկցիայի նշանապահպանման միջակայքերն են։

Ֆունկցիայի գրաֆիկը 3 կետից ձախ պետք է գտնվի աբսցիսների առանցքից վերև, իսկ (3, 5) և (5, +∞) միջակայքերում՝ ներքև։ Ֆունկցիան 3 և 5 կետերում ընդունում է 0 արժեքը, այսինքն՝ հատում է աբսցիսների առանցքը։ Այդպիսի բազմաթիվ ֆունկցիաներ կան։ Դրանցից մի քանիսը պատկերված են ստորև.

Առաջադրանքներ․

1)Գտե՛ք պատկերված գրաֆիկով ֆունկցիայի նշանապահպանման միջակայքերը․

(- ∞;-1) +

(-1;3) —

(3;∞) +

(-∞;-2) —

(-2;2) +

(2;∞) +

(-∞;2) +

(2;0) +

(0;3) —

(3;∞) +

(-∞;-2) —

(-2;2) +

(2;3) —

(3;∞) +

(-∞;-3) +

(-3;2) —

(2;∞) +

(-∞;-2) —

(-2;1) +

(1;∞) +

2)Գծե՛ք ֆունկցիայի գրաֆիկ, որի նշանապահպանման միջակայքերը կլինեն․

ա) (−∞, −2), (−2, 1), (1, +∞),

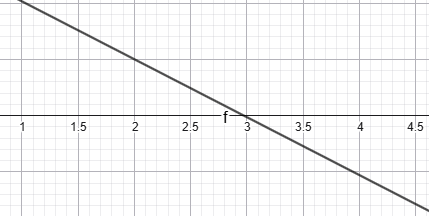
բ) (−∞; 3), (3; +∞),

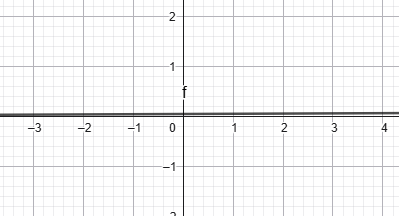
գ) (−∞, +∞):

3)Գծե՛ք ֆունկցիայի գրաֆիկ, որի նշանապահպանման միջակայքերի գծապատկերը կունենա հետևյալ տեսքը․

4)Ճարտարապետ Ռաֆայելը տարվա ընթացքում նախագծեց 25 առանձնատուն՝ 10 փոքր ու 15 մեծ։Փոքր առանձնատներից յուրաքանչյուրի համար նա վաստակում է 240 000 դրամ, իսկ մեծի համար՝ 450 000։
ա) Մեկ պատվերից միջինում որքա՞ն գումար է աշխատում Ռաֆայելը։
բ) Շինարարության ընթացքում Ռաֆայելը փոքր առանձնատուն այցելում է 7 անգամ, իսկ մեծ առանձնատուն՝ 12։ Յուրաքանչյուր այցելության ժամանակ նա ծախսում է միջինում 1500 դրամի մեքենայի վառելիք։ Տարվա ընթացքում որքա՞ն շահույթ ստացավ Ռաֆայելը։

5)Գտնել (-5; 36) միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

6)Գտնել (34; 78) միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

7)Գտնել (23; 57] միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

8)Գտնել [-3; 45) միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

9)Գտնել [23; 123] միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։