ՖՈՒՆԿՑԻԱՅԻ ԳՐԱՖԻԿԻ ՏԵՂԱՇԱՐԺԵՐԸ

у = f(x) + a ֆունկցիայի գրաֆիկը у = f(x) ֆունկցիայի գրաֆիկի միջոցով կառուցելիս տեղի է ունենում գրաֆիկի տեղաշարժ օրդինատների առանցքի ուղղությամբ:

— Տեղաշարժի ուղղությունը (դեպի վերև կամ դեպի ներքև) որոշվում է a թվի նշանով:

— Տեղաշարժի չափը որոշվում է a թվի մոդուլի արժեքով:

Եթե a > 0, ապա գրաֆիկը տեղաշարժվում է դեպի վերև, իսկ եթե a < 0, ապա՝ դեպի ներքև:

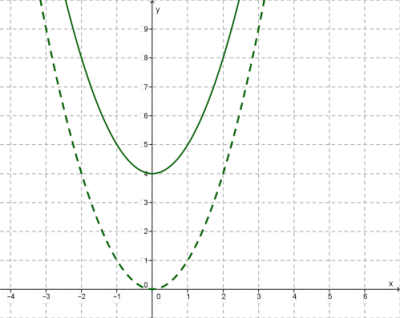
Այս նկարում կատարվում է у = x² ֆունկցիայի գրաֆիկի տեղաշարժ` չորս միավորով դեպի վերև: Ուրեմն, սա у = x² + 4 ֆունկցիայի գրաֆիկն է:

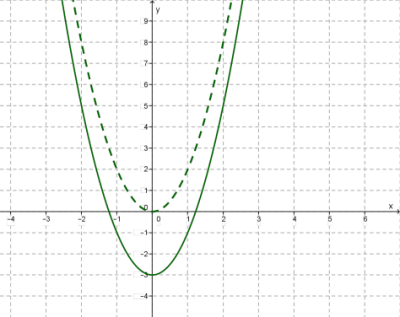
Այս նկարում կատարվում է у = x² ֆունկցիայի գրաֆիկի տեղաշարժ` երեք միավորով դեպի ներքև: Ուրեմն, սա у = x² − 3 ֆունկցիայի գրաֆիկն է:

Ճիշտ է հետևյալ պնդումը:

1) y = f(x) + a, որտեղ a-ն տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել y = f(x) ֆունկցիայի գրաֆիկը y-երի առանցքի ուղղությամբ՝ a միավորով դեպի վերև:

2) y = f(x) − a, որտեղ a-ն տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել y = f(x) ֆունկցիայի գրաֆիկը y-երի առանցքի ուղղությամբ՝ a միավորով դեպի ներքև:

Առաջադրանքներ․

1)Դիցուք, f(x) ֆունկցիայի գրաֆիկը տեղաշարժեցին 5 միավորով վերև, այնուհետև՝ 7 միավորով ներքև։ Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց։

y=f(x)-2

2)Դիցուք, f(x) ֆունկցիայի գրաֆիկը տեղաշարժեցին − 2 միավորով ա) վերև, բ) ներքև։ Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց։

1.y=f(x)-2

2.y=f(x)+2

3)Հայտնի է, որ f(x) ֆունկցիայի արժեքների տիրույթը [0, ∞) միջակայքն է: Գտե՛ք g(x) = f(x) + 3 ֆունկցիայի արժեքների տիրույթը:

[3,∞)

4)Դիցուք f(x) ֆունկցիայի արժեքների տիրույթը [−4, −1] միջակայքն է։ Գտե՛ք.
ա) g(x) = f(x) − 2.5, [-6.5)
բ) g(x) = f(x) + 2 ֆունկցիայի արժեքների տիրույթը

5)Նկարում պատկերված է ֆունկցիայի գրաֆիկը։ Պատկերե՛ք f(x) + 1 և f(x) — 3 ֆունկցիաների գրաֆիկները:

ա)