1)
(a5)2=(a2)5
(a3)4=(a2)6
(a6)7=(a2)21
2)
1.11*(27-12)=11*2-5 =11*1/25 =11*32
2.5*(315-11)=5*34=5*27
1)
(a5)2=(a2)5
(a3)4=(a2)6
(a6)7=(a2)21
2)
1.11*(27-12)=11*2-5 =11*1/25 =11*32
2.5*(315-11)=5*34=5*27
Ֆեռնանդո Կորտես դե Մոնրոյ ի Պիսառո Ալտամիրանո է Ֆեռնանդո, Էռնանդո, Ֆեռնան կամ Էռնան Կորտես (իսպ.՝ Hernán Cortés) անուններով, որը նվաճել է Մեքսիկան և ոչնչացրել ացտեկների պետությունը։ Կառլոս V կայսրը Կորտեսին շնորհել է Marqués del Valle de Oaxaca (հայերեն տառադարձությամբ՝ Մարկես դել Վալյե դե Օախակա, թարգմանաբար՝ Օախակա հովտի մարկիզ) կոչում։ Նրա շնորհիվ Եվրոպայում 1520 թվականից սկսել են օգտագործել վանիլ և շոկոլադ[5]։
Էռնան Կորտեսը ոչ շատ հարուստ, բայց ազնվական իդալգոների ընտանիքից էր։ Երկու տարի սովորել է Սալամանկայի համալսարանում, սակայն գերադասել է ռազմական կարիերան։ 1504 թվականին տեղափոխվել է Էսպանյոլա, 1510—1514 թվականներին Դիեգո դե Վելասկեսի գլխավորությամբ մասնակցել է Կուբայի նվաճման արշավին։ 1519—1521 թվականներին սեփական նախաձեռնությամբ սկսել է Մեքսիկայի նվաճումը։ 1522—1526 թվականներին նորաստեղծ Նոր Իսպանիա գաղութում զբաղեցրել է գեներալ-կապիտանի պաշտոնը՝ այնտեղ անցկացնելով անկախ քաղաքականություն, սակայն իշխանության համար կատաղի պայքարի պատճառով 1528 թվականին վերադարձել է Եվրոպա։
Քրիստոֆեր Կոլումբոս — 1492 թվականին Կոլումբոսը առաջին եվրոպացին էր, ով հասավ Ամերիկա՝ փնտրելով նոր ճանապարհներ դեպի Հնդկաստան։ Նրա ճանապարհորդությունը հանգեցրեց եվրոպացիների համար նոր աշխարհների բացմանը։
Ֆերդինանդ Մագելլան — 1519-1522 թվականներին Մագելլանը կազմակերպեց առաջին աշխարհը շրջանցող ճանապարհորդությունը։ Նա առաջինն էր, ով անցկացրեց նախշով օվկիանոսներից մեկով՝ Շրջելով աշխարհը։
Հերման Կորտես — 1519 թվականին Կորտեսը հասավ Մեքսիկա, որտեղ նա հանդիպեց Ազտեկների կայսրությանը։ Նրա արշավը հանգեցրեց ոչ միայն Ազտեկների ոչնչացման, այլ նաև մեքսիկական մշակույթի եվրոպականացման։
Աբել Թասման — 1642-1644 թվականներին Թասմանն առաջին եվրոպացին էր, ով հասավ Նոր Զելանդիա և Թահիտին։ Նրա հայտնագործությունները մեծ դեր խաղացին օվկիանոսի քարտեզագրման գործում։
Ջեյմս קוק — 18-րդ դարի նշանավոր ծովագնացի, ով ուսումնասիրել է Պասիֆիկ օվկիանոսը, Վրաստան, Հավայան կղզիները և Ավստրալիան։ Նրա ճանապարհորդությունները օգնել են քարտեզագրել անծանոթ տարածքներ։
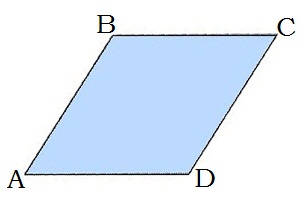
Շեղանկյուն կոչվում է այն զուգահեռագիծը, որի բոլոր կողմերը հավասար են:
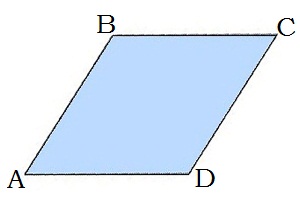
Շեղանկյան հատկությունները․
Քանի որ շեղանկյունը զուգահեռագիծ է, ապա այն ունի զուգահեռագծի բոլոր հատկությունները:
1. Շեղանկյան հանդիպակաց կողմերը հավասար են՝ AB=BC=CD=AD (քանի որ հավասար են բոլոր կողմերը):
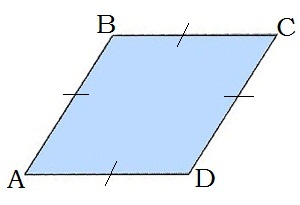
2. Շեղանկյան հանդիպակաց անկյունները հավասար են՝ ∢A=∢C, ∢B=∢D:
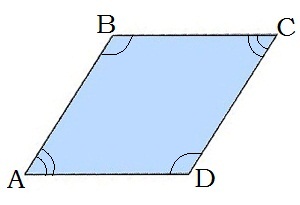
3. Շեղանկյան անկյունագծերը հատման կետով կիսվում են՝ BO=OD, AO=OC
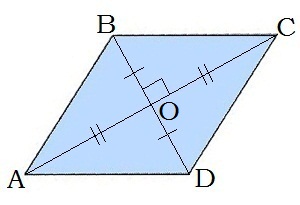
4. Շեղանկյան կողմին առընթեր անկյունների գումարը 180° է՝ ∢A+∢D=180°
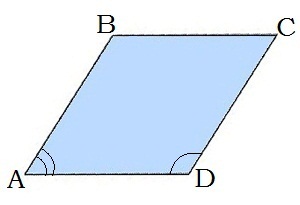
Միայն շեղանկյանը բնորոշ հատկություններ.
5. Շեղանկյան անկյունագծերը փոխուղղահայաց են՝ AC⊥BD
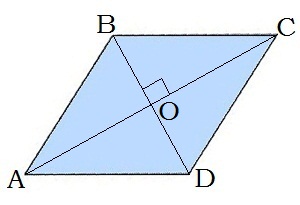
6. Շեղանկյան անկյունագծերը նաև անկյունների կիսորդներ են (անկյունները կիսում են)
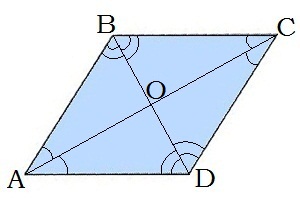
7. Անկյունագծերը շեղանկյունը բաժանում են չորս հավասար ուղղանկյուն եռանկյունների՝ ABO, CBO, CDO, ADO եռանկյունները հավասար ուղղանկյուն եռանկյուններ են:
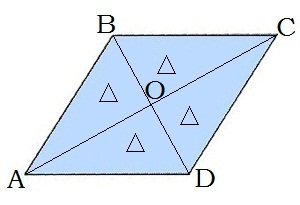
Քառակուսի է կոչվում այն ուղղանկյունը, որի բոլոր կողմերը հավասար են:
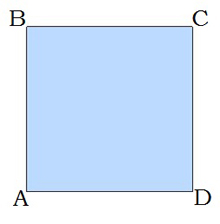
Քառակուսու հատկությունները․
1. Քառակուսու բոլոր կողմերը հավասար են՝ AB=BC=CD=AD:
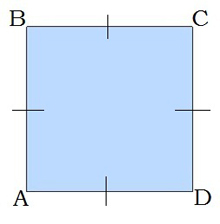
2. Քառակուսու բոլոր անկյունները 90° են:
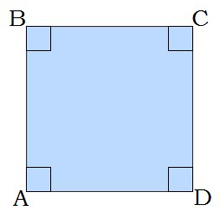
3. Քառակուսու անկյունագծերը հավասար են և հատման կետով կիսվում են՝ BD=AC; BO=OD=AO=OC:
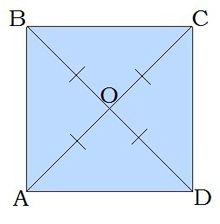
4. Քառակուսու անկյունագծերը փոխուղղահայաց են՝ BD⊥AC:
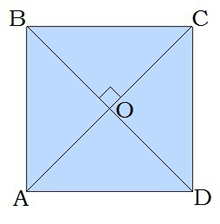
5. Քառակուսու անկյունագծերը նաև անկյունների կիսորդներ են՝ ∢ABD=∢DBC=∢BCA=…=45°:
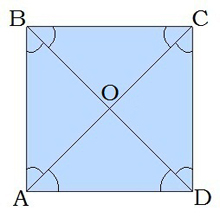
6. Անկյունագիծը քառակուսին բաժանում է չորս հավասար հավասարասրուն ուղղանկյուն եռանկյունների:
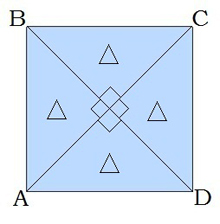
Առաջադրանքներ․
1)Քառակուսու անկյունագծերի հատման կետից մինչև կողմերը եղած հեռավորությունների գումարը 20 սմ է։ Գտեք քառակուսու պարագիծը։
20*4=80
p=80
2)Շեղանկյան անկյուններից մեկը 2 անգամ մեծ է մյուսից: Հաշվիր շեղանկյան անկյունները:

x+2x=180
2x+2x+x+x
180:3=60
60×2=120
x=60
2x=120
3)Հաշվիր շեղանկյան սուր անկյունը, եթե նրա երկու անկյունների տարբերությունը 18° է:

180-18=12
162:2=81
81+18=99
4)Հաշվիր շեղանկյան բութ անկյունը, եթե նրա անկյունագծերից մեկը կողմի հետ կազմում է 31° -ի անկյուն:
31+31=62
180-62=118
5)Շեղանկյան սուր անկյունը հավասար է 60°, իսկ պարագիծը 48 մ է: Հաշվիր շեղանկյան փոքր անկյունագիծը:
48:4=12
60:2=30
Լրացուցիչ աշխատանք (տանը)․
1)Քառակուսու պարագիծը 72 սմ է: Հաշվիր քառակուսու կողմը:
2)Հաշվիր շեղանկյան պարագիծը, եթե նրա կողմի երկարությունը 4.45 դմ է:
3)Տրված է՝ OD=3 սմ, AC=14 սմ: Գտիր BD-ն և AO-ն:

4)Հաշվիր շեղանկյան մյուս անկյունները, եթե A անկյունը 67° է:
5)Հոկտեմբեր ամսվա մաթեմատիկական ֆլեշմոբ․
Հետևյալ նյութերից առանձնացրեք օքսիդները, հիմքերը, նշեք յուրաքանչյուրի անվանումը. HNO3, Na2O, Ca(OH)2, AgNO3, BaO, HCl, CO2, Al2O3, NaHCO3, Fe(OH)2, K2SiO3, NaCl, H2SO4, MgO, NaOH, H3PO4, SO3, CaCl2, CuSO4, Al(OH)3.
h-no
na-o
ca-on
ag-no
ba-o
h-cl
al-o
1.a-1 2.a1
3.a4 4.a
5.a-10 6.a9
7.a1 8.a9
9.a-3 10.a-8
1.27 2.56
3.4 5 4.7 7
5.3 13 6.613
7.166 8.915
1.5/62 2.2/29 3.25/494 4.m/a7 5.m/a8 6.n/a12
Մարդը հասարակական էակ է: Հասարակության մեջ ձևավորվում են նրա պահանջմունքները և դրանք բացարելուն ուղղված հմտություններն ու կարողությունները: Յուրանքանչյուր էակ որևէ ընտանիքի, համայնքի ազգի ներկայացուցիչ է:
Որոշ էակներ, որոնք գիտեն իրենց այս կամ այն կատեգորիայի պատկանելիության մասին, փոխազդում են միմյանց հետ և կազմում են սոցիալական համայնք: Սոցիալական համայնքի ամենակարևոր ձևը սոցիալական խումբն է:
Սոցիալական խումբը այն անհատների կատեգորիան է, որտեղ որոշակի կերպով փոխազդում են միմյանց հետ, զգում են իրենց պատկանելությունը այդ խմբին և ուրիշների կողմից ընկալվում են որպես տվյալ խմբի անդամներ: Կան խմբեր, որտեղ էակն ընգրկվում է իրենց կամքից անկախ, օրինակ.՝ ըստ սեռի և տարիքի, ըստ բնակության վայրի, ըստ զբաղմունքի, մասնագիտության և այլն:
Помню себя маленьким — четырёхлетним, может быть, трёхлетним. Вижу себя в окружении вещей, которые не только будят во мне какие-то мысли, но и действуют на мои чувства. Вот сутулый шкаф стоит, подпирая своей широкой спиной стену, погрузившись в бесконечную думу. От него не добьёшься слов. Если он и произнесёт что-нибудь на своём скрипучем, непонятном для меня языке, то лишь когда открывают дверцы, чтоб достать что-нибудь из одежды.
По сравнению со шкафом буфет — легкомысленное существо. У него и цвет не такой серо-бурый, а с красноватым отливом. Верхние дверцы на его груди украшены деревянной резьбой. По бокам торчат выточенные из дерева шпилеобразные фигуры, напоминающие шахматных ферзей. Этот чудак буфет, наверно, воображает, что очень красиво, когда на плечах такие нелепые штуковины. На его полках хранятся сахар, печенье, варенье, иногда даже конфеты. И кофейная мельница — её можно вертеть сколько угодно, когда никто не видит.
Словом, буфет — существо нелепое, но компанейское, чего не скажешь о креслах. В белых чехлах, из-под которых, точно из-под платьев, торчат только кончики ножек, они похожи на чопорных дам. Они чинно сидят по углам комнаты и молчат. Чувствуется, что им до зарезу хочется поговорить. Хочется посудачить о разном, да не хочется показывать, что их могут интересовать пустые разговоры. В их обществе я чувствую себя лишним, чем-то вроде гвоздя в сапоге.
Вопросы к представленному тексту:
1.Почему взрослые часто не понимают детей, согласно тексту?-Взрослые часто не понимают детей, потому что видят мир не таким, каким его видят дети.
2. Как различается восприятие предметов взрослыми и детьми?-В окружающих предметах взрослые видят их назначение Дети же видят лицо вещей. Они не знают, откуда эти вещи явились,
3. Как описания предметов передают эмоции автора?
Он радостный
4. Как эти эмоции помогают понять внутренний мир автора?
5. Как описания предметов могут отражать культурные или социальные нормы?
6. Какие черты характера автора проявляются через его описания вещей?-любопыстбо
7. Какой урок или послание можно извлечь из текста о восприятии мира детьми и взрослыми?-