Рубрика: հանրահաշիվ

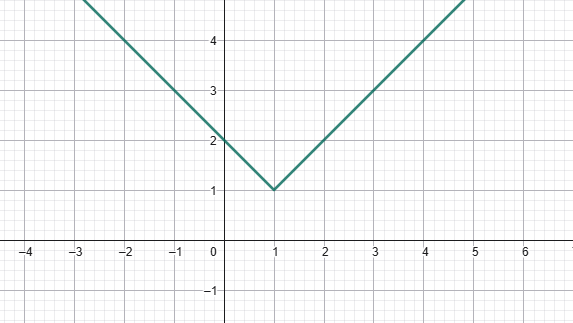
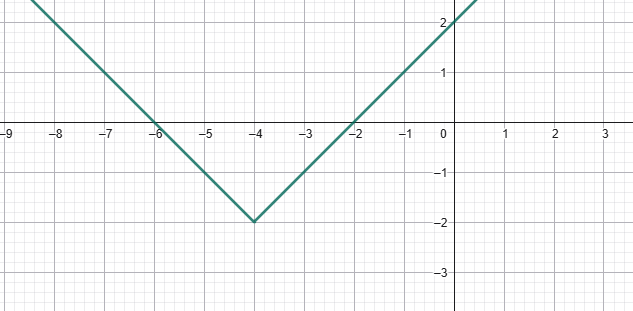
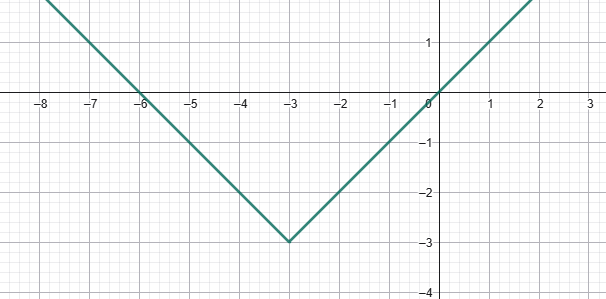
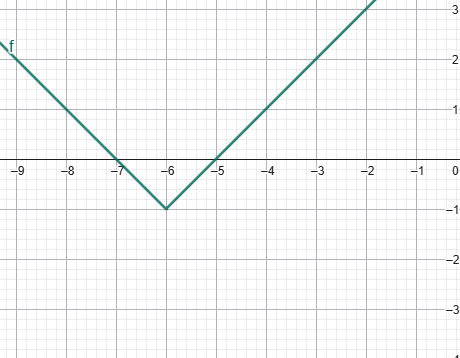
Համակարգչային ծրագրերով գծելով y = √x ֆունկցիայի գրաֆիկը՝ ստանում ենք հետևյալ պատկերը․

Նշենք գրաֆիկի որոշ առանձնահատկություններ և փորձենք բացատրել դրանք․
1)Գրաֆիկն անցնում է կոորդինատների սկզբնակետով։ Պատճառն այն է, որ x = 0 դեպքում y = √0 = 0։
2)Որոշման տիրույթը [0, +∞) բազմությունն է: Իսկապես, արմատատակ արտահայտությունը բացասական լինել չի կարող։
3)Բացի (0, 0) կետից, ֆունկցիայի գրաֆիկի բոլոր կետերը գտնվում են կոորդինատային հարթության առաջին քառորդում։ Իսկապես, x > 0 դեպքում y = √(x) > 0: ֆունկցիայի գրաֆիկի կետերի կոորդինատները դրական են:
4)Ֆունկցիան աճող է: Եթե x₂ > x₁ > 0, ապա √x₂ > √x₁, այսինքն՝ ֆունկցիայի արգումենտի մեծ արժեքին համապատասխանում է ֆունկցիայի մեծ արժեք:

y = √x ֆունկցիայի գրաֆիկի միջոցով կարող ենք կառուցել y = √(x-3) և y = √x — 4 ֆունկցիաների գրաֆիկները: Եթե f(x) = √x, ապա y = √(x-3) բանաձևը կարող գրել այսպես` y = f(x — 3): Մենք գիտենք, որ f(x — 3) ֆունկցիայի գրաֆիկը ստանալու համար պետք է y = f(x) ֆունկցիայի գրաֆիկը երեք միավորով տեղաշարժել աջ:

y = √x — 4 ֆունկցիայի գրաֆիկը գծելու համար բավական է նկատել, որ y = f(x) — 4 այսինքն՝ f(x)-ի գրաֆիկից 4 միավորով ներքև է:

Ինչպես պարաբոլի ու մոդուլի դեպքում, այստեղ ևս վերև/ներքև ու աջ/ձախ տեղաշարժերը հնարավոր է համատեղել։
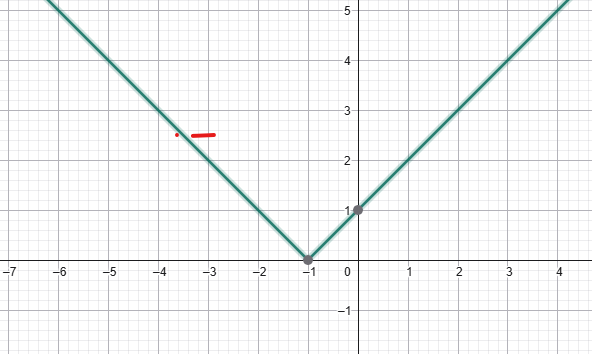
Նկարում պատկերված է y = √(x+1) + 3 ֆունկցիայի գրաֆիկը:

Առաջադրանքներ․

1)Տրված է f(x) = √(x — 2) + 1 ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) 6, բ) 2, գ) 4 կետում:

f(x) = √(6— 2) + 1=3

f(x) = √(2 — 2) + 1=0

f(x) = √(4 — 2) + 1=√2+1

2)Տրված է f(x) = √(x + 1) ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) 0, բ) -1, գ) 8 կետում:

f(x) = √(x + 1)=√1

f(x) = √(x + 1)=0

f(x) = √(x + 1)=3

3)Տրված է f(x) = -√(2x) ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 3, բ) —1, գ) –10 արժեքը:

f(x) = -√(2x)=լուծում չունի

f(x) = -√(2x) =1/2

f(x) = -√(2x) =50

4)Տրված է f(x) = -√(x+6)ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) −1, բ) 0, գ) −4, դ) 3 արժեքը:

f(x) = -√(x+6)=-5

f(x) = -√(x+6)=-6

f(x) = -√(x+6)=-2

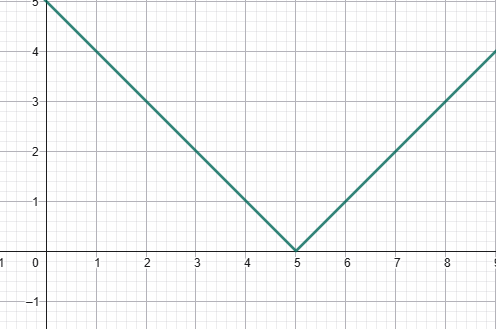
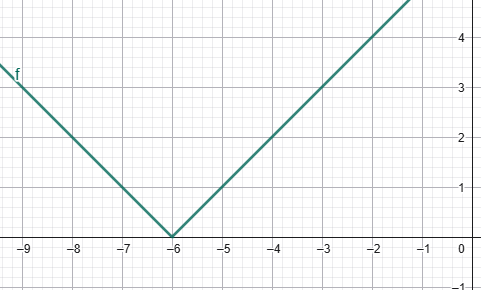
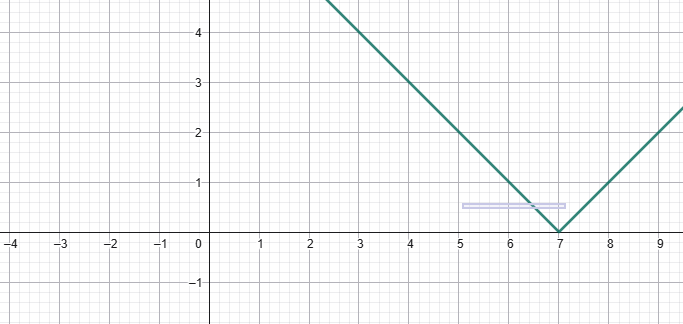
5)Նկարում պատկերված է y =√(x — x₀) + y₀ ֆունկցիայի գրաֆիկը: Գտե՛ք x₀ և y₀ թվերը.

6)Կառուցե՛ք ֆունկցիայի գրաֆիկը.

ա) y = √(x) — 2
բ) y = √(x) + 3
գ) y = √(x + 5)
դ) y = √(x — 3) + 5
ե) y = √(x + 2) — 8
զ) y = — √(x — 10) + 6

1)Գտե՛ք ֆունկցիայի զրոները.
ա) y = |x|
բ) y = |x + 2| — 8
6,-10
գ) y = — 2|x| — 4
լուծում չունի
դ) y = 3|x — 1| — 6
3,-1
ե) y = 0.5|x + 2| — 3
4,-8
զ) y = — 5|x| + 10
-2,2

2)Գծե՛ք ֆունկցիայի գրաֆիկը.
ա) y = |x + 1|

բ) y = |x — 5|

գ) y = |x + 6|

դ) y = |x — 3|

3)Գծե՛ք ֆունկցիայի գրաֆիկը.
ա) y = |x| + 1

բ) y = |x| + 4

գ) y = |x| — 3

դ) y= |x| — 1

4)Գծե՛ք ֆունկցիայի գրաֆիկը.
ա) y = |x — 1| + 1

բ) y = |x + 4| — 2

գ) y = |x — 3| — 3

դ) y = |x + 6| — 1

1, 2, 4, 8, 16, … հաջորդականության ամեն անդամ, սկսած երկրորդից, իր նախորդից մեծ է 2 անգամ: 1, 10, 100, 1000, … հաջորդականությունում կա նմանատիպ օրինաչափություն. հաջորդ անդամը նախորդից մեծ է 10 անգամ։ Նմանատիպ հաջորդականություններն անվանում են երկրաչափական պրոգրեսիաներ:

Զրոյից տարբեր թվերի հաջորդականությունն անվանում ենք q հայտարարով երկրաչափական պրոգրեսիա, եթե հաջորդականության յուրաքանչյուր հաջորդ անդամ, սկսած երկրորդից, ստացվում է իր նախորդը q-ով բազմապատկելով: q-ն անվանում ենք երկրաչափական պրոգրեսիայի հայտարար:

1, 2, 4, 8, 16, … և 1, 10, 100, 1000,… հաջորդականությունները համապատասխանաբար q = 2 և q = 10 հայտարարներով երկրաչափական պրոգրեսիաներ են: q հայտարարով {a_n} երկրաչափական պրոգրեսիայի համար տեղի ունի
a_{n + 1} = a_n * q

Օրինակ 1.
{a_n} երկրաչափական պրոգրեսիայում a₃ = 6 q = 1/3, հաշվենք a₄ — ը:
a₄ = a₃ * q = 6 * 1/3 = 2

Օրինակ 2.
{a_n} երկրաչափական պրոգրեսիայում a₁ = 8 և q = 1.5, հաշվենք a₄ — ը:
a₂ = a₁* q = 8 * 1.5 = 12
a₃ = a₂* q = 12 * 1.5 = 18
a₄ = a₃ *q = 18 * 1.5 = 27

Օրինակ 2-ում կարող ենք a₄-ն արտահայտել a₁-ով ու q-ով՝ առանց հաշվելու a₂
-ի և a₃-ի արժեքները.

$$a_4=a_3\ast q=(a_2\ast q)\ast q=a_2\ast q^2=(a_1\ast q)\ast q^2=a_1\ast q^3$$

Ստացված a₄ = a₁* q³ բանաձևը կարող ենք ընդհանրացնել երկրաչափական պրոգրեսիայի ցանկացած համար: a_n-ը ստանալու համար պետք է a₁ — ը (n-1) անգամ բազմապատկել q-ով.

a_n = a₁ * q * q * . . . * q = a₁ * q^n-1

Դրական անդամներից կազմված երկրաչափական պրոգրեսիայի ցանկացած անդամ (բացառությամբ առաջինի) հավասար է իր երկու հարևանների միջին երկրաչափականին (n ≥ 2):

Առաջադրանքներ․

1)Տրված է 1, 3, 9, 27, … երկրաչափական պրոգրեսիան։ Գտեք նրա հայտարարը և հինգերորդ, վեցերորդ ու յոթերորդ անդամները:

1, 3, 9, 27,81, 243, 729

2)Հաջորդականությունն արդյոք երկրաչափական պրոգրեսիա՞ է.
ա) 1, 8, 15, 21, 26, …; ոչ
բ) 4, 2, 1, 0,5, 0,25, …; ոչ
գ) -2, 2, -2, 2, -2, …; այո
դ) 0, 4, 16, 64, 256, …: այո

3)Գտեք a_n երկրաչափական պրոգրեսիայի առաջին չորս անդամները, եթե a₁ = 2, q = 0,25 :

2×0,25=0,5

05, 0.125, 0.03125

4)Տրված է a_n երկրաչափական պրոգրեսիան։ Հաշվեք.

a_n  = a₁ * q^n-1
ա)a₃ — ը, եթե a₁= 0,5, q = — 2; -2
բ)a₄ — ը, եթե a₁ = -2, q = 3; = -54
գ) a₃ — ը և q — ն, եթե a₁ = 3, a₂ = 4; -16/3
դ) a₃ — ը և q — ն, եթե a₁ = — 4, a₂ = 6 = -9

5)Տրված են երկրաչափական պրոգրեսիայի երեք իրար հաջորդող անդամներ.
ա) 7, x, 63։ Գտեք x — ը, եթե x > 0 : x=21
բ) 2, x, 18։ Գտեք x — ը, եթե x < 0 : x=11.225
գ) 3,2; x; 0,2։ Գտեք x — ը ։ -0,8

Հաջորդականությունն անվանում ենք d տարբերությամբ թվաբանական պրոգրեսիա, եթե հաջորդականության յուրաքանչյուր անդամ, սկսած երկրորդից, ստացվում է իր նախորդին d գումարելով։ d-ն անվանում ենք թվաբանական պրոգրեսիայի տարբերություն։

d տարբերությամբ թվաբանական պրոգրեսիայի համար տեղի ունի a_{n + 1} = a_n + d հավասարությունը: Թվաբանական պրոգրեսիայի ընդհանուր անդամի բանաձևը.

a_n = a₁ + d(n — 1)

Օրինակ 1.
Գրենք թվաբանական պրոգրեսիայի a₁, a₂,…,a₆ անդամները, եթե տրված է, որ a₁ = — 2, d = 4:
Հաջորդականության յուրաքանչյուր հաջորդ անդամը նախորդից մեծ է 4-ով։ Հաջոր-դականության երկրորդ անդամն է.
a₂ = a₁ + d = — 2 + 4 = 2, իսկ երրորդ անդամն է a₃ = a₂ + d = 2 + 4 = 6: Շարունակելով ստանում ենք հետևյալ հաջորդականությունը. -2, 2, 6, 10, 14, 18, …:

{a_n} թվաբանական պրոգրեսիայի առաջին ո անդամների գումարն ընդունված է նշանակել S_n — ով.
S_n = a₁ + a₂ +…+a_n

Պարզվում է, որ տրված հաջորդականության համար կա S_n-ը հաշվելու բանաձև.

S_n = n * (a₁ + a_n)/2

Տեղադրելով a_n = a₁ + d(n — 1)-ն S_n -ի բանաձևի մեջ, կստանանք․

S_n = n * (a₁ + a₁ + d(n — 1))/2 = n * (2a₁ + d(n — 1))/2

Օրինակ 2․

{a_n} թվաբանական պրոգրեսիայում ա) a₁ = 5, a₁₀ = 8: Հաշվենք S₁₀ — ը:

S₁₀ = 10 * (a₁ + a₁₀)/2 = 65

Օրինակ 3․

{a_n} թվաբանական պրոգրեսիայում a₁ = 3 d = -7: Հաշվենք S₁₀ — ը:

S₁₀ = 10 * (2 *3 + (10 — 1)(-7))/2 = 10 * (-57)/2 = -285

Առաջադրանքներ․

1)Գտե՛ք տրված թվաբանական պրոգրեսիայի տարբերությունը.

ա) 9, 11, 13, 15,
տերբերությւն=2
բ) 1, 0, -1, -2
տարբերությունը=-1
գ) 3, 7, 11, 15,
տարբերությունը=-3
դ) 4, 1, -2, -5,
տարբերությունը=-4
ե) 1, 1.5, 2, 2.5,
տարբերությունը=0.5
զ) 7.5, 6.2, 4.9, 3.6,
տարբերությունը=-0.13

2)Տրված է {a_n} թվաբանական պրոգրեսիայի անդամներից ինչ-որ մեկը և d տարբերությունը: Գտե՛ք պրոգրեսիայի առաջին չորս անդամները.

ա)a₁ = 2 d = 5
2-5=3
բ)a₁ = 9 d = — 3
9-3=6
գ)a₂ = — 2 d = 1.5
-2+1.5=-0.5
դ)a₃ = — 7 d = — 3.5
-7+-3.5=-3.5

3)Տրված է {a_n} թվաբանական պրոգրեսիան։ Հաշվե՛ք.

ա)S₁₂ — ը, եթե a₁ = 5, a₁₂ = 35
20×12=240
բ)S₉ — ը, եթե a₁ = 4, a₉ = 28
16×9=144
գ)S₁₇ — ը, եթե a₁ = 4, a₁₇ = 45
24.5×17=416.5
դ)S₅ — ը, եթե a₁ = 2, a₅ = -8
-3×5=-15

4)Տրված է {a_n} թվաբանական պրոգրեսիան։ Հաշվե՛ք.

ա)S₁₀ — ը, եթե a₁ = 3, d = 4
S10= 6+4(10-1)/2×10 =210
բ)S₈ — ը, եթե a₁ = 7, d = 1
S8=14-1(8-1)/2×8=80
գ)S₁₃ — ը, եթե a₁ = 4, d = -1
S13=8+-1(13-1)/2×13=
դ)S₅ — ը, եթե a₁ = -4, d = 2

Անվերջ քանակությամբ թվերի կարգավորված հերթականությունն անվանում ենք թվային հաջորդականություն կամ պարզապես հաջորդականություն։

Հաջորդականությունը գրելու համար օգտագործում են լատիներեն այբուբենի որևէ տառ, որը համարակալվում է ինդեքսով՝ a₁, a₂, a₃, . . . : Հաջորդականության թվերն անվանում են հաջորդականության անդամներ: a_n-ը անվանում են հաջորդականության ո-րդ անդամ (n-ը բնական թիվ է):

Թվային հաջորդականության բոլոր թվերը գրել հնարավոր չէ, անհրաժեշտ է ինչ որ կերպ նկարագրել այն։ Տալ հաջորդականությունը` նշանակում է նկարագրել, թե ինչպես գտնել հաջորդականության ո-րդ անդամը: Հաջորդականությունը տալու հիմնական եղանակներն են՝ օրինաչափությամբ և բանաձևային:

Օրինակ 1.

Գտեք 2, 3, 5, 7, 11, 13, 17, 19, 23, …, օրինաչափությունն ու 10-րդ անդամը:
Հաջորդականությունում գրված են պարզ թվերը՝ փոքրից մեծ: 23-ին հաջորդող պարզ թիվը 29-ն է։

Օրինակ 2.

Գտնենք հաջորդականության 5-րդ անդամը:
ա)a_n = n + √n
բ) a_n = (- 1)ⁿ/(n + 3)
Լուծում․
ա) a₅ = 5 + √5
բ) a₅ = (- 1)⁵ /5 + 3 = -1/8

Առաջադրանքներ․

1)Գտե՛ք օրինաչափությունը և հաջորդականության հաջորդ անդամը.
ա) 1, 11, 111, 1111, 11111,
բ) 1,-2, 3, 4, 5, -6, 7,
գ) 1, 0, 1, 0, 1, 0, 1, 0,
դ) 1, 2, 3, 1, 2, 3, 1, 2,
ե) 1, 2, 4, 5, 7, 8, 10, 11, 13,
զ) 1, 2, 2, 3, 3, 3, 4, 4:

2)Գրե՛ք բանաձևով տրված հաջորդականության առաջին 5 անդամը.
ա)a_n = 2n + 1 2×1+1
բ)a_n = 7(n — 2) 2×2+1
գ)a_n = — 4n + 2 3×2+1
դ)a_n = 1.5n + 2 4×2+1
ե)a_n = 3ⁿ 5×2+1
զ)a_n = 6 * 2^{n — 1} 6×2+!

3)Հաշվե՛ք n-րդ անդամի բանաձևով տրված հաջորդականության երրորդ և չորրորդ անդամները.
ա) a_n = (n — 3)⁵
բ) b_n = (n + 1)^{n — 4}
գ) e_n = (- 1)ⁿ * n

4)Տրված է հաջորդականության n-րդ անդամի բանաձևը.
ա) a_n = 3n — 1 Գտեք a₁, a₂, a₅ , a₁₀₀ -ը։
բ)a_n = 3 + 2(n — 1) Գտեք a₁, a₂, a₁₂ , a₃₀ -ը։

5)Գտեք ընդհանուր անդամի բանաձևով տրված հաջորդականության առաջին վեց անդամների գումարը.
ա) a_n = 3n + 2
բ) a_n = (- 1)ⁿ * n

ax⁴ + bx² + c = 0 տեսքի հավասարումը, որտեղ a, b, c տրված թվեր են, ընդ որում՝ a ≠ 0, անվանում ենք երկքառակուսային հավասարում:

Երկքառակուսային հավասարումը լուծելու համար կատարում ենք y = x² նշանակումը:

Օրինակ 1․
Լուծենք x⁴ — 6x² + 5 = 0 երկքառակուսային հավասարումը:
y = x² նշանակմամբ ստանում ենք y² — 6y + 5 = 0 քառակուսային հավասարումը: Այս հավասարումն ունի երկու լուծում՝ y = 1 և y = 5։

Վերադառնալով x փոփոխականին՝ ստանում ենք հետևյալ համախումբը՝

Համախմբի հավասարումներն ունեն երկուական լուծումներ՝ x = ± 1 և x = ± √5: Այսպիսով, գտանք հավասարման բոլոր լուծումները՝ x ϵ {-√5, -1, 1, √5}:

Առաջադրանքներ․

1)Փոփոխականի փոխարինմամբ ստացե՛ք քառակուսային հավասարում.
ա) (x + 2)² + 5(x + 2) — 3 = 0

(y)²+5(y)-3

բ) (x — 4)² — 3(x — 4) + 1 = 0

(a)²-3(a)+1

գ) 2(x — 3)² — (x — 3) + 5 = 0

2(b)²-(b)+5

դ) 2(x + 7)² — 4(x + 7) — 1 = 0

2(c)²-4(c)-7

2)Փոփոխականի փոխարինմամբ լուծե՛ք հավասարումը.
ա) (x — 4)² + 6(x — 4) + 5 = 0

x=3
x=-1
բ) (x + 1)² — 7(x + 1) — 18 = 0

x=8
x=-3
գ) (x — 1)² + 8(x — 1) + 12 = 0

x=-5
x=-1

դ) (4z + 3)² — (4z + 3) — 2 = 0


x=1/4
x=-1

3)Փոփոխականի փոխարինմամբ ստացե՛ք քառակուսային հավասարում.
ա) a⁴ + 5a² — 7 = 0

y²+5y-y=0

բ) 4x⁴ + 9x² — 1 = 0

y²+y-1=0

գ) 5x⁴ + 9x²— 12 = 0

y²+y-12=0

դ) -2b⁴ + 7b² + 1 = 0

-y²+y+1=0

A(x) * B(x) = 0 տեսքի հավասարումը, որտեղ A(x)-ը և B(x)-ը x-ի նկատմամբ բազմանդամներ են, անվանում ենք վերածվող հավասարում:

Օրինակ՝ (x² + 5)(x³ — 6x + 7) = 0 վերածվող հավասարում է, մինչդեռ (x² + 5)(x³ — 6x ) + 7 = 0 հավասարումը՝ ոչ:
A(x) ∙ B(x) = 0 վերածվող հավասարումը համարժեք է

համախմբին, քանի որ A(x) ∙ B(x) արտադրյալը հավասար է 0-ի, երբ արտադրիչներից գոնե մեկը 0 է:

Օրինակ 1.
Լուծենք (x — 2)(x² — x + 7) = 0 վերածվող հավասարումը:
Հավասարումը գրենք համարժեք համախմբի տեսքով.

Համախմբի առաջին հավասարման լուծումն է x = 2: Երկրորդ հավասարման տարբերիչը բացասական է՝ D = (- 1)² — 4 ∙ 1 ∙ 7 = — 27 հետևաբար այն լուծում չունի: Այսպիսով, համախումբն ունի մեկ լուծում՝ x = 2:

Օրինակ 2.
Լուծենք (x² + 5)(x — 3)(x² — 4x + 3) = 0 հավասարումը: Հավասարումը
գրենք համախմբի տեսքով.

Համախմբի առաջին հավասարումը լուծում չունի, երկրորդն ունի մեկ լուծում՝ x = 3 իսկ երրորդը՝ երկու լուծում՝ x = 1 և x = 3: Այդ լուծումների բազմությունների միավորումից ստացվում են հավասարման արմատները՝ x = 1 և x = 3` x∈{1;3}:

Առաջադրանքներ․

1)Լուծե՛ք վերածվող հավասարումը.

ա) (x + 5)(x — 7) = 0

-5,7
բ) 4x² = 0

0

գ) 2(x — 5)² = 0

+5

դ) (3x + 12)(4 — x) = 0

-4,4

ե) — 2x²(x + 1) = 0

0,-1

զ) (5 — x)(x — 9) = 0

+5,+9

2)Լուծեք հավասարումը․

ա)(x² + 5x + 6)(x + 2) = 0

25-4x1x6=1

x1=-b+√D/2a=-5+1/2=-2

x2=-b-√D/2a=1,-2

բ)(x² — 9x + 14)(x — 7) = 0

81-4x1x14

գ)(x² + 7x + 10)(x² — 25) = 0

դ)(x² — 7x + 12)(x² — 6x + 10) = 0

ե)(x² — 15x — 16)(x² + 8x + 7) = 0

զ)(x² — 4x + 3)(x² + 4x + 3) = 0

1)Շրջանագծի հատողն իր արտաքին մասից մեծ է 2ամբ1/4 անգամ։ Հատողը նույն կետից տարված շոշափողից քանի՞ անգամ է մեծ։

ab:ad=9/4^2

3/2

2)Դիցուք՝ AB-ն շոշափող է, AD-ն՝ նույն շրջանագծի հատող, որի արտաքին մասը AC-ն է։ Որոշեք՝
ա) CD-ն, եթե AB = 2 սմ և AD = 4 սմ
4×2=8
բ) AD-ն, եթե AC : CD = 4/5 և AB = 12 սմ
9×2=18

3)Մի կետից շրջանագծին տարված շոշափողն ու հատողը համապատասխանաբար հավասար են 20 սմ և 40 սմ, իսկ հատողի հեռավորությունը շրջանագծի կենտրոնից՝ 8 սմ։ Գտեք շրջանագծի շառավիղը։

17

4)Մի կետից շրջանագծին տարված են հատող և շոշափող: Որոշեք շոշափողի երկարությունը, եթե նա հատողի արտաքին մասից 5 սմ–ով մեծ է, իսկ ներքին մասից` նույնքանով փոքր:

5)Մի կետից նույն շրջանագծին տարված են երկու հատող՝ որոնց երկարություններն են 15 սմ և 25 սմ։ Գտեք նրանց արտաքին մասերը, եթե հայտնի է, որ դրանցից մեկը 2 սմ–ով մեծ է մյուսից։

Համակարգը ճիշտ է, երբ ճիշտ են համակարգի բոլոր պայմանները` լինի հավասարում թե անհավասարում։ Այդ պատճառով էլ համակարգի լուծումն իր առանձին պայմանների լուծումների բազմությունների հատումն է։
Օրինակ 1․

Լուծենք համակարգը․

Առաջին անհավասարման լուծումն է (- ∞, — 1] U [3, ∞) բազմությունը, իսկ երկրորդինը՝ (— 2, 4) բաց միջակայքը: Իրար տակ գծենք կոորդինատային առանցքներ և առանձին-առանձին պատկերենք անհավասարումների լուծումները:

Համակարգի լուծումն այդ լուծումների բազմությունների հատումն է՝ (-2, -1] U [3, 4) բազմությունը:

Օրինակ 2.

Լուծենք համախումբը.

Համախումբը կազմված է երկու անհավասարումից: Առաջին անհավասարման լուծումը (-∞, 1) U(5, +∞) բազմությունն է, իսկ երկրորդինը՝ [2,5]: Կոորդինատային առանցքների վրա պատկերելով այդ բազմությունները՝ հեշտությամբ կգտնենք դրանց միավորումը՝ (-∞, 1) U [2, +∞):

Օրինակ 3.

Լուծենք համախումբը.

Կոորդինատային առանցքների վրա պատկերենք անհավասարումների լուծումները.
Առաջին անհավասարման լուծումը` (-∞, -1) U (-1,0) U (3,+∞);
Երկրորդ անհավասարման լուծումը՝ (− 4, 1]։
Համախմբի լուծումն այդ երկու բազմությունների միավորումն է՝ (-∞, 1] U (3,+∞):

Նկատենք, որ −4 թիվը համախմբի լուծում է, թեև x-ի այդ արժեքի դեպքում համախմբի երկրորդ անհավասարումն իմաստ չունի:

Առաջադրանքներ․

1)Լուծե՛ք անհավասարումների համակարգը.

1.(-an;-5)(1;+an) [6;7]

2.(-an;7)(1;+an) [4;10]

3.(-an;4)(1;+an) [2;5]

2)Լուծե՛ք անհավասարումների համակարգը.

1.-3; 5, 3 +an

2.0;-6, 6;+an

3.-an;1, 3;6

3)Լուծե՛ք անհավասարումների համախումբը.

1.-an;6, 7 +an

2.-an;1, 5;+an

3.-an;3, 9;+an

1)Լուծեք անհավասարումները․

1.+-+

2.-++

3.++-

4.-+-

2)Լուծեք անհավասարումները․

1.+++

2.+-+

3.++-

4.-+_

3)Լուծեք անհավասարումները․

1.++-

2.—+

3.+-+-

4.—+

4)Լուծեք անհավասարումները․

1.+_+-

2.+—+

3.—+-

4.+-+-

5)Լուծեք անհավասարումները․

1.+++-

2.-+++

3.+-+-

4.-+-+