Рубрика: հանրահաշիվ

Խորանարդների գումարը արտադրիչների վերլուծելու համար օգտագործվում է

a³ + b³ = (a + b) (a² — ab + b²)            ( 1 )

նույնությունը, որը կոչվում է խորանարդների գումարի բանաձև:

Օրինակ 1: Արտադրիչների վերլուծենք 27x³ + y³ բազմանդամը:

Տվյալ բազմանդամը հնարավոր է ներկայացնել երկու արտահայտությունների խորանարդների գումարի տեսքով.

27x³ + y³ = (3x)³ + y³:

Կիրառելով (1) բանաձևը կստանանք.

(3x) ³ + y³ = (3x + y) (9x² — 3xy + y²):

Եվ այսպես՝

27x³ + y³ = (3x + y) (9x² — 3xy + y²):

Խորանարդների տարբերությունը արտադրիչների վերլեւծելու համար օգտագործվում է

a³ — b³ = (a – b) (a² + ab + b²)            ( 2 )

նույնությունը, որը կոչվում է խորանարդների տարբերության բանաձև:

Օրինակ 2: Արտադրիչների վերլուծենք m⁶ — n³ բազմանդամը:
Տվյալ բազմանդամը ներկայացնենք երկու արտահայտությունների խորանարդների տարբերության տեսքով և կիրառենք (2) բանաձևը: Կստանանք՝

m⁶ — n³ = (m²)³ — n³ = (m² — n) (m⁴ + m²n + n²):

Առաջադրանքներ

1)Միանդամը ներկայացրո՛ւ խորանարդի տեսքով․

125-5³

8=2³

27x³=(3x)³

64y³=(4y)³

M³y³=(my)³

A⁶b³=(a²b)³

(xy²)³

2)Հաշվի՛ր օգտվելով Խորանարդների գումարի բանաձևից՝
a³ + b³ = (a + b) (a² — ab + b²)            ( 1 )

(x+2)(x²-2x+2²)

(3+a)(3²-3a+a²)

4)Հաշվի՛ր օգտվելով Խորանարդների գումարի բանաձևից՝
(a + b) (a² — ab + b²)=a³ + b³

Խորանարդների գումարը արտադրիչների վերլուծելու համար օգտագործվում է

a³ + b³ = (a + b) (a² — ab + b²)            ( 1 )

նույնությունը, որը կոչվում է խորանարդների գումարի բանաձև:

Օրինակ 1: Արտադրիչների վերլուծենք 27x³ + y³ բազմանդամը:

Տվյալ բազմանդամը հնարավոր է ներկայացնել երկու արտահայտությունների խորանարդների գումարի տեսքով.

27x³ + y³ = (3x)³ + y³:

Կիրառելով (1) բանաձևը կստանանք.

(3x) ³ + y³ = (3x + y) (9x² — 3xy + y²):

Եվ այսպես՝

27x³ + y³ = (3x + y) (9x² — 3xy + y²):

Խորանարդների տարբերությունը արտադրիչների վերլեւծելու համար օգտագործվում է

a³ — b³ = (a – b) (a² + ab + b²)            ( 2 )

նույնությունը, որը կոչվում է խորանարդների տարբերության բանաձև:

Օրինակ 2: Արտադրիչների վերլուծենք m⁶ — n³ բազմանդամը:
Տվյալ բազմանդամը ներկայացնենք երկու արտահայտությունների խորանարդների տարբերության տեսքով և կիրառենք (2) բանաձևը: Կստանանք՝

m⁶ — n³ = (m²)³ — n³ = (m² — n) (m⁴ + m²n + n²):

Առաջադրանքներ

1)Միանդամը ներկայացրո՛ւ խորանարդի տեսքով․

125-5³

8=2³

27x³=(3x)³

64y³=(4y)³

M³y³=(my)³

A⁶b³=(a²b)³

(xy²)³

2)Հաշվի՛ր օգտվելով Խորանարդների գումարի բանաձևից՝
a³ + b³ = (a + b) (a² — ab + b²)            ( 1 )

(x+2)(x²-2x+2²)

(3+a)(3²-3a+a²)

(1+m)(1²-1m+m²)

(p+4)(p²-p4+4²)

(x+2y)(x²-x2+2²)

(a+3b)(a²-27ab+27b²)

(2m+x)(2²-2mx+2m²)

3)Հաշվի՛ր օգտվելով Խորանարդների գումարի բանաձևից՝
(a + b) (a² — ab + b²)=a³ + b³

M³+n³

Q³+p³

A³+3³

8³+x³

P²+64³

25³+m³

Հիշե՛ք․

(a+b)² = a²+2ab+b²

(a−b)²=a²−2ab+b²

 a²−b² = (a−b)

1)Օգտվելով գումարի քառակուսու բանաձևից՝ բացե՛ք փակագծերը.

ա) (a ² + b)²=a⁴ +2a²b+b²

բ) (3x ² + 1)²=9x⁴+6x²+1

գ) (x ² + y ²)²=x⁴+2x²y²+y⁴

դ) (2x+a³)²=4x²+4xa³+a⁶

2)Աստղանիշի փոխարեն գրե՛ք միանդամներ, որպեսզի ստացվի ճիշտ
հավասարություն.

ա) (a + 3b)² = a ² + 2ab + 9b²

բ) (x + 1)² = x + 6x + 1,

գ) (x + y)² = x ² + 2xy + y²

3)Արտահայտությունը ներկայացրե՛ք բազմանդամի քառակուսու (գումարի քառակուսու) տեսքով.

ա) x ² + 6x + 9 =(x+3)²

բ) 4a⁴ + 8a²b + 4b² =(2a²+2b)

գ) 4a ² + 4a + 1 =(2a+1)

դ) m² + 10m + 25 =(m+5)

4)Արտահայտությունը ձևափոխե՛ք կատարյալ տեսքի բազմանդամի.

ա) (a − b)² + (a + b)² =a²-2ab+b²+a²+2ab+b²=2a²+2b²

բ) (x − 3)² + (x − 2)(x − 4) =x²— 6x+9+x²-4x-2x+8=2x²-12x+17

2.a²+6a+9+a²+2a+1=2a²+8a+10

3.(m²+2m+1)*2+(m²+4m+4)*3=5m²+16m+14

4.(p²+2pq+q²)*5+(p²+4pq+4q)*3=8p²+22pq+17q²

5.2a²+10ab+9b-3a²+10ab+4b=-5a²+20ab+5b

6.(3x²+6xy+y²)*2-(2x²+10xy+9y)*3=6x²-18xy-20y²

7.

8.

1.(m+n)(m+n)=m²+mn+nm+n²

2.(2+x)(2+x)=4+2x+2x+x²=4+4x²+x²

3.(y+4)(y+4)=y²+4y+4y+16=y²+8y²+16

4.(1+p)(1+p)=1+1p+1p+1=2+2p

5.(2x+1)(2x+1)=4x²+2+2x+1

6.(2+3a)(2+3a)=4+6a+6a+9²=4+12a²+9²

7.(3m+5n)(3m+5n)=9m²+15mn+15nm+25n²

8.(3x+4y)(3x+4y)=9x²+12xy+12yx+16y²

1.(a²+b)(a²+b)=a⁴+a²b++ba²+b²

2.(p³+q⁵)(p³+q⁵)=p⁹+pq⁸+qp⁸+q¹⁰          

3.(3m+n³)(3m+n³)=9m²+3mn³+3mn³+n⁹=9m²+9mn⁹+n⁹

4.(ab+c)(ab+c)=ab²+abc+cab+c²

5.(2p+3q²)(2p+3q²)=2p²+5pq²+5q²p+9q⁴

6.(x+yx)(x+yx)=x²+x²y+yx²+yx²

7.(3ab²+2c³)(3ab²+2c³)=9ab⁴+5ab²c³+5ab²c³+4c⁹

1.(1/2+a)(1/2+a)=1/2²+1/2a+1/2a+a²=1/2²+2/4a²+a²

2.(x+1/3)(x+1/3)=x²+1/3x+1/3x+1/3²=x²+2/6+1/3²

3.(m+0,2)(m+0,2)=m²+0,2m+0,2m+0,2²=m²+0,4²+0,2²

4.(1,1+p)(1,1+p)=1,1²+1,1p+1,1p+p²=1,1²+2,2p²+p²

5.(1/2a+2/3b)(1/2a+2/3b)=1/2a²+3/5ab+3/5ab+2/3b²=1/2²+6/10ab²+2/3b²

6.(3/4x+1/5y)(3/4x+1/5y)=6/8x²+9/12xy+4/9yx+1/5y²

7.(0,2m+2,1n)(0,2m+2,1n)=0,2m²+2,3mn+2,3mn+2,1n²=0,2m²+4,6mn²+2,1n²

8.(0,4p+0,3q)(0,4p+0,3q)=0,4p²+0,7pq+0,7pq+0,3q²=0,4p²+0,14pq²+0,3q²

1.(a+2b)(a+2b)=a²+2ba+2ba+4b²=a²+4ba²+4b²

2.(3x+y)(3x+y)=3x²+3xy+3xy+y²=3x²+9xy++y²

3.(2x+3y)(2x+3y)=2x²+5xy+5yx+3y²

4.(x+2)(x+2)=x²+2x+2x+2²=x²4x²+2²

Ամբողջ արտահայտություն և նրա թվային արժեք

4 декабря 2023Հանրահաշիվ 7-9

Հանրահաշվական արտահայտություն կոչվում է իմաստալից կազմված գրառումը տառերի, թվաբանական գործողությունների, թվերի և փակագծերի մասնակցությամբ:

a²−3b-ն հանրահաշվական արտահայտություն է:

Քանի որ հանրահաշվական արտահայտության մեջ մասնակցող տառերը կարող են ընդունել տարբեր թվային արժեքներ, ապա տառերը կոչվում են փոփոխականներ:

Թվային արտահայտության պարզեցման արդյունքում ստացվում է թիվ, որը կոչվում է թվային արտահայտության արժեք:

Հաշվենք a²−3b հանրահաշվական արտահայտության արժեքը a=−16 և b=−14 դեպքում․

a²−3b=(−16)²−3⋅(−14)=256+42=298

Իսկ a²−3a+2 հանրահաշվական արտահայտության արժեքը a=−4 դեպքում հավասար է 30-ի, քանի որ՝

(−4)²−3(−4)+2=16+12+2=30

Եթե տառերի որոշակի արժեքների դեպքում հանրահաշվական արտահայտությունն ունի թվային արժեք, ապա փոփոխականի այդ արժեքները կոչվում են թույլատրելի:

(a²−3)/(a+2) հանրահաշվական արտահայտության համար a=−4-ը թույլատրելի է, իսկ a=−2-ը թույլատրելի չէ, քանի որ այդ դեպքում պետք է բաժանել զրոյի վրա, իսկ զրոյի վրա բաժանել չի կարելի:

Առաջադրանքներ․

1)Հաշվել ամբողջ արտահայության արժեքը x = -10 դեպքում․

ա)3x — 8=3 *(-10)-8=-38

բ)3x² + 4x + 1= 300-40+1=261 

գ)x⁴ + 2x³ + 8x² + x=10000-2000+800-10=8790

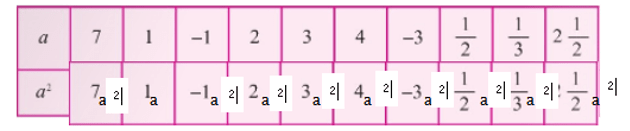
2)Լրացրեք աղյուսակը

3)Հաշվեք արտահայտության արժեքը․

ա)(2xy² — 3a)(4x — 5a³y)= եթե x = 1, y = -1, a = 2

բ)(x³ yz² — 4xy³)(3x²y³ — 5xy²z³) եթե x = 2, y = -1, z = -1

գ)(a + b — c)(a² — b²) եթե a = 3, b = 2, c = -4

Լրացուցիչ աշխատանք (տանը)․

1)Գտեք ամբողջ արտահայտության արժեքը a = -1; b = 2; c = 3 դեպքում․

ա)abc=-1x2x3=-6

բ)ab²c³=-1×2²x3³=-10

գ)3a²(bc)=3ax2x3=8a

դ)(2ab)³c²=2abx3=5ab

ե)(a² — b²) — 3c=1-2×3=4

զ)7(a³ — b²)² + c³=1-2×3=4

2)Լրացրեք աղյուսակը․

3)Հաշվեք արտահայտության արժեքը․

ա)(3a² b — 5x)(7a — 4bx²) եթե a = 1, b = 1, x = 1

բ)(a²b²c — 3b⁵c³)(5a³bc⁴ + 7ab⁴c) եթե a = -1, b = -1, c = -1

գ)(a + b + c)(a² + b²) եթե a = -3, b = -2, c = 4

1)Բազմանդամը վերլուծեք արտադրիչների․

ա)2x + 2y =2(x+y)

բ)6a — 3 =3(2a-1)

գ)ax — ab =a(x-b)

դ)2a + 6ab =2a(1+3b)

ե)a² + a =a(a+a)

զ)3x³ — xy² =x(3x² -y²)

է)ax + bx + cx =x(a+b+c)

ը)5a³ + 10a² + 15a=5a(a² +2a+3)

2)Վերլուծե՛ք արտադրիչների.

ա) x(b + a) + y(a + b) =(a+b)(x+y)

բ) 7x(a − b) − 8y(a − b) =(a-b)(7x-8y)

գ) 5y(z − 4) + 2x(4 − z) =(4-z)(5y-2x)

դ) 5x(2a − 7b) + 6y(7b − 2a) =(2a-7b)(5x-6y)

ե) 4a(3x − 1) − b(1 − 3x) =(3x-1)(4a+b)

զ) 7a(a − 3) − (3 − a)(1 + b) =(a-3)(1+b+7a)

Լրացուցիչ աշխատանք (տանը)․

Բազմանդամը վերլուծեք արտադրիչների․

ա)x(a + b) + y(a + b)=(a+b)(x+y)

բ)m(n — 3) — 2(n — 3)=(n-3)(m-2)

գ)(a + b)a — b(a + b)=^(a+b)(a-b)

դ)(x — y)3 — a(x + b)=(x-y)(3-a)

ե)2a(1 — b) — 3(1 — b)=(1-b)(2a-3)

զ)a(b + 3) — b(3 + b)=(b+3)(a-b)  

է)7x( x + 2y) — 2(2y + x)=(x+2y)(7x-2)

ը)a(a + b) + (a + b)=a(a+b)

Բացե՛ք փակագծերն ու բերե՛ք կատարյալ տեսքի.

ա) (x + 3)(x + 6)=x²+6x+3x+18=x²+9x+18,

բ) (3a + 4)(2a – 7)=6a²-21a+8a-28=6a²-13a-28,

գ) (9x² − 4x)(9x + 4)=81x³+36x²-36x²-16x=81x³-16x,

դ) (2y² − b²)(3y² + 4b²)=6y⁴+8y²-3b²y²-4b⁴

ե) (a − b)(a + b),=a²+ab-ba-b²

զ) (7a − 3)(7b + 3)=7ab+21a-21b-9:

2)Բացե՛ք փակագծերն ու միավորե՛ք նման միանդամները.

ա) (ax + 5)(bx − 1)abx²+1ax+5bx+5,

բ) (7b² + 3a³)(3a³ − 7b²)=21b²a³+39b⁴3a⁶+21a³b²,

գ) (y − 2)(y + 1),=y²+1y-2y-2

դ) (−x + 5)(x − 1):=-x²-1x+5x+5

3)Բերե՛ք կատարյալ տեսքի.

ա) 5(2 − 3c) + 7(3c + 1),

բ) 6x(x − 2) − 3(2x² − 4),

գ) (a + b)( a² − ab + b²),

դ) (x + 1)(y + 1) + (x − 1)(y − 1):