Рубрика: հանրահաշիվ

ax⁴ + bx² + c = 0 տեսքի հավասարումը, որտեղ a, b, c տրված թվեր են, ընդ որում՝ a ≠ 0, անվանում ենք երկքառակուսային հավասարում:

Երկքառակուսային հավասարումը լուծելու համար կատարում ենք y = x² նշանակումը:

Օրինակ 1․
Լուծենք x⁴ — 6x² + 5 = 0 երկքառակուսային հավասարումը:
y = x² նշանակմամբ ստանում ենք y² — 6y + 5 = 0 քառակուսային հավասարումը: Այս հավասարումն ունի երկու լուծում՝ y = 1 և y = 5։

Վերադառնալով x փոփոխականին՝ ստանում ենք հետևյալ համախումբը՝

Համախմբի հավասարումներն ունեն երկուական լուծումներ՝ x = ± 1 և x = ± √5: Այսպիսով, գտանք հավասարման բոլոր լուծումները՝ x ϵ {-√5, -1, 1, √5}:

Առաջադրանքներ․

1)Փոփոխականի փոխարինմամբ ստացե՛ք քառակուսային հավասարում.
ա) (x + 2)² + 5(x + 2) — 3 = 0

(y)²+5(y)-3

բ) (x — 4)² — 3(x — 4) + 1 = 0

(a)²-3(a)+1

գ) 2(x — 3)² — (x — 3) + 5 = 0

2(b)²-(b)+5

դ) 2(x + 7)² — 4(x + 7) — 1 = 0

2(c)²-4(c)-7

2)Փոփոխականի փոխարինմամբ լուծե՛ք հավասարումը.
ա) (x — 4)² + 6(x — 4) + 5 = 0

x=3
x=-1
բ) (x + 1)² — 7(x + 1) — 18 = 0

x=8
x=-3
գ) (x — 1)² + 8(x — 1) + 12 = 0

x=-5
x=-1

դ) (4z + 3)² — (4z + 3) — 2 = 0


x=1/4
x=-1

3)Փոփոխականի փոխարինմամբ ստացե՛ք քառակուսային հավասարում.
ա) a⁴ + 5a² — 7 = 0

y²+5y-y=0

բ) 4x⁴ + 9x² — 1 = 0

y²+y-1=0

գ) 5x⁴ + 9x²— 12 = 0

y²+y-12=0

դ) -2b⁴ + 7b² + 1 = 0

-y²+y+1=0

A(x) * B(x) = 0 տեսքի հավասարումը, որտեղ A(x)-ը և B(x)-ը x-ի նկատմամբ բազմանդամներ են, անվանում ենք վերածվող հավասարում:

Օրինակ՝ (x² + 5)(x³ — 6x + 7) = 0 վերածվող հավասարում է, մինչդեռ (x² + 5)(x³ — 6x ) + 7 = 0 հավասարումը՝ ոչ:
A(x) ∙ B(x) = 0 վերածվող հավասարումը համարժեք է

համախմբին, քանի որ A(x) ∙ B(x) արտադրյալը հավասար է 0-ի, երբ արտադրիչներից գոնե մեկը 0 է:

Օրինակ 1.
Լուծենք (x — 2)(x² — x + 7) = 0 վերածվող հավասարումը:
Հավասարումը գրենք համարժեք համախմբի տեսքով.

Համախմբի առաջին հավասարման լուծումն է x = 2: Երկրորդ հավասարման տարբերիչը բացասական է՝ D = (- 1)² — 4 ∙ 1 ∙ 7 = — 27 հետևաբար այն լուծում չունի: Այսպիսով, համախումբն ունի մեկ լուծում՝ x = 2:

Օրինակ 2.
Լուծենք (x² + 5)(x — 3)(x² — 4x + 3) = 0 հավասարումը: Հավասարումը
գրենք համախմբի տեսքով.

Համախմբի առաջին հավասարումը լուծում չունի, երկրորդն ունի մեկ լուծում՝ x = 3 իսկ երրորդը՝ երկու լուծում՝ x = 1 և x = 3: Այդ լուծումների բազմությունների միավորումից ստացվում են հավասարման արմատները՝ x = 1 և x = 3` x∈{1;3}:

Առաջադրանքներ․

1)Լուծե՛ք վերածվող հավասարումը.

ա) (x + 5)(x — 7) = 0

-5,7
բ) 4x² = 0

0

գ) 2(x — 5)² = 0

+5

դ) (3x + 12)(4 — x) = 0

-4,4

ե) — 2x²(x + 1) = 0

0,-1

զ) (5 — x)(x — 9) = 0

+5,+9

2)Լուծեք հավասարումը․

ա)(x² + 5x + 6)(x + 2) = 0

25-4x1x6=1

x1=-b+√D/2a=-5+1/2=-2

x2=-b-√D/2a=1,-2

բ)(x² — 9x + 14)(x — 7) = 0

81-4x1x14

գ)(x² + 7x + 10)(x² — 25) = 0

դ)(x² — 7x + 12)(x² — 6x + 10) = 0

ե)(x² — 15x — 16)(x² + 8x + 7) = 0

զ)(x² — 4x + 3)(x² + 4x + 3) = 0

1)Շրջանագծի հատողն իր արտաքին մասից մեծ է 2ամբ1/4 անգամ։ Հատողը նույն կետից տարված շոշափողից քանի՞ անգամ է մեծ։

ab:ad=9/4^2

3/2

2)Դիցուք՝ AB-ն շոշափող է, AD-ն՝ նույն շրջանագծի հատող, որի արտաքին մասը AC-ն է։ Որոշեք՝
ա) CD-ն, եթե AB = 2 սմ և AD = 4 սմ
4×2=8
բ) AD-ն, եթե AC : CD = 4/5 և AB = 12 սմ
9×2=18

3)Մի կետից շրջանագծին տարված շոշափողն ու հատողը համապատասխանաբար հավասար են 20 սմ և 40 սմ, իսկ հատողի հեռավորությունը շրջանագծի կենտրոնից՝ 8 սմ։ Գտեք շրջանագծի շառավիղը։

17

4)Մի կետից շրջանագծին տարված են հատող և շոշափող: Որոշեք շոշափողի երկարությունը, եթե նա հատողի արտաքին մասից 5 սմ–ով մեծ է, իսկ ներքին մասից` նույնքանով փոքր:

5)Մի կետից նույն շրջանագծին տարված են երկու հատող՝ որոնց երկարություններն են 15 սմ և 25 սմ։ Գտեք նրանց արտաքին մասերը, եթե հայտնի է, որ դրանցից մեկը 2 սմ–ով մեծ է մյուսից։

Համակարգը ճիշտ է, երբ ճիշտ են համակարգի բոլոր պայմանները` լինի հավասարում թե անհավասարում։ Այդ պատճառով էլ համակարգի լուծումն իր առանձին պայմանների լուծումների բազմությունների հատումն է։
Օրինակ 1․

Լուծենք համակարգը․

Առաջին անհավասարման լուծումն է (- ∞, — 1] U [3, ∞) բազմությունը, իսկ երկրորդինը՝ (— 2, 4) բաց միջակայքը: Իրար տակ գծենք կոորդինատային առանցքներ և առանձին-առանձին պատկերենք անհավասարումների լուծումները:

Համակարգի լուծումն այդ լուծումների բազմությունների հատումն է՝ (-2, -1] U [3, 4) բազմությունը:

Օրինակ 2.

Լուծենք համախումբը.

Համախումբը կազմված է երկու անհավասարումից: Առաջին անհավասարման լուծումը (-∞, 1) U(5, +∞) բազմությունն է, իսկ երկրորդինը՝ [2,5]: Կոորդինատային առանցքների վրա պատկերելով այդ բազմությունները՝ հեշտությամբ կգտնենք դրանց միավորումը՝ (-∞, 1) U [2, +∞):

Օրինակ 3.

Լուծենք համախումբը.

Կոորդինատային առանցքների վրա պատկերենք անհավասարումների լուծումները.
Առաջին անհավասարման լուծումը` (-∞, -1) U (-1,0) U (3,+∞);
Երկրորդ անհավասարման լուծումը՝ (− 4, 1]։
Համախմբի լուծումն այդ երկու բազմությունների միավորումն է՝ (-∞, 1] U (3,+∞):

Նկատենք, որ −4 թիվը համախմբի լուծում է, թեև x-ի այդ արժեքի դեպքում համախմբի երկրորդ անհավասարումն իմաստ չունի:

Առաջադրանքներ․

1)Լուծե՛ք անհավասարումների համակարգը.

1.(-an;-5)(1;+an) [6;7]

2.(-an;7)(1;+an) [4;10]

3.(-an;4)(1;+an) [2;5]

2)Լուծե՛ք անհավասարումների համակարգը.

1.-3; 5, 3 +an

2.0;-6, 6;+an

3.-an;1, 3;6

3)Լուծե՛ք անհավասարումների համախումբը.

1.-an;6, 7 +an

2.-an;1, 5;+an

3.-an;3, 9;+an

1)Լուծեք անհավասարումները․

1.+-+

2.-++

3.++-

4.-+-

2)Լուծեք անհավասարումները․

1.+++

2.+-+

3.++-

4.-+_

3)Լուծեք անհավասարումները․

1.++-

2.—+

3.+-+-

4.—+

4)Լուծեք անհավասարումները․

1.+_+-

2.+—+

3.—+-

4.+-+-

5)Լուծեք անհավասարումները․

1.+++-

2.-+++

3.+-+-

4.-+-+

Օրինակ 1.
Լուծենք անհավասարումը. 2x² — 9x + 7 > 0
Անհավասարման ձախ մասը վերլուծենք արտադրիչների.
2x² — 9x + 7 = 0
D = (- 9)² — 4 * 2 * 7 = 25
x₁ = (9 — 5)/(2 * 2) = 1
x₂ = (9 + 5)/(2 * 2) = 3.5
Փաստորեն, ստանում ենք հետևյալ համարժեք անհավասարումը.
2(x — 1)(x — 3.5) > 0
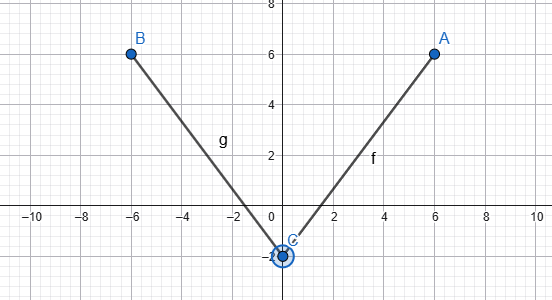
Անհավասարման լուծումներն x-ի այն արժեքներն են, որոնց դեպքում 2(x — 1)(x — 3.5) արտահայտության արժեքը դրական է։ Այդ արժեքները կարող ենք գտնել երկու եղանակով՝ միջակայքերի ու գրաֆիկական:
Միջակայքերի եղանակ`
Որոշենք 2(x — 1)(x — 3.5) արտահայտության նշանապահպանման միջակայքերը:

(- ∞, 1) և (3.5, +0) միջակայքերում արտահայտությունը դրական է։ Այդ միջակայքերի միավորումը՝ (- ∞, 1) U (3.5, +∞) բազմությունը, կլինի անհավասարման լուծումը: Բազմությունը կարող ենք պատկերել կոորդինատային առանցքի վրա: 1 և 3.5 կետերը նշված են ոչ հոծ (դատարկ), քանի որ անհավասարման լուծումներ չեն.

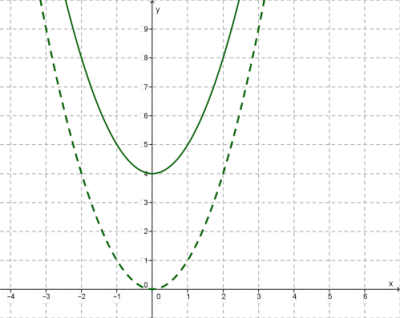
Գրաֆիկական եղանակ`
Գծենք y = 2(x — 1)(x — 3.5) ֆունկցիայի գրաֆիկը: Պարաբոլի ճյուղերն ուղղված են վերև, իսկ x-երի առանցքը հատում է 1 և 3.5 կետերում։ Գրաֆիկը կունենա նկարում պատկերված տեսքը: Ֆունկցիայի արժեքը դրական է (- ∞, 1) U (3.5, +∞) բազմության
կետերում:

Օրինակ 2.
Լուծենք x² — 7x + 10 <= 0 անհավասարումը։
Բազմանդամի արմատներն են 2 և 5 թվերը: Այն վերլուծելով արտադրիչների՝ ստանում ենք հետևյալ անհավասարումը.
(x — 2)(x — 5) <= 0
Ուսումնասիրելով նշանապահպանման միջակայքերը՝ տեսնում ենք, որ (2, 5) միջակայքում արտահայտությունը բացասական է։ Քանի որ արտահայտությունն ընդունում է 0 արժեքը 2 և 5 կետերում, ուրեմն լուծումը կլինի [2, 5] հատվածը (փակ միջակայքը).

Օրինակ 3.
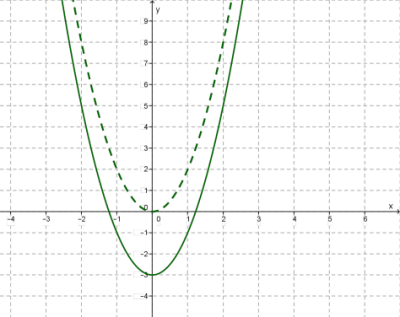
Լուծենք 2x² — 7x + 6 >= 0 անհավասարումը:
Քանի որ 2x² — 7x + 6 = 2(x — 1.5)(x — 2) ուրեմն՝ y = 2x² — 7x + 6 ֆունկցիայի գրաֆիկն ունի նկարում պատկերված տեսքը:

Ինչպես տեսնում ենք, ֆունկցիայի գրաֆիկն ընդունում է ոչ բացասական արժեքներ (- ∞, 1.5] և [2, ∞) կիսաբաց միջակայքերում։ Այդ բազմությունների միավորումը՝ (−∞, 1.5] U [2, +∞)-ը կլինի անհավասարման լուծումը.

Առաջադրանքներ․

1)Անհավասարումը լուծե՛ք միջակայքերի եղանակով.
ա) x² — 6x + 5 > 0
0.7
բ) — x² + 9x + 10 >= 0
1.25
գ) 3x² + 12x + 4 <= — 5
1.66
դ) 4x² + 14x — 5 > — 15

1.8

2)Անհավասարումը լուծե՛ք գրաֆիկական եղանակով.
ա) x² + 6x — 7 > 0
0
բ) — x² + 4x — 3 <= 0
3
գ) — 4x² — 6x + 5 >= 7
1
դ) 4x² + x + 8 >= 24 — 11x

2

3)Լուծե՛ք անհավասարումը.
ա) (x — 6)(x + 9) < 0
+—
բ) (x + 4)(x — 3) >= 0
-+-
գ) (x — 5)(x + 1) >= 0
++-
դ) (2x + 5)(x + 5) <= 0
—+
ե) — 3(x + 1)(x — 5) > 0

+-+
զ) — 2(x + 4)(x — 3.25) <= 0

-+-

1)Հաշվել արտահայտության արժեքը․

1.11/7

2.29/39

3.-1/20

4.1/9

2)Հաշվել արտահայտության արժեքը․

ա)|5a + 2| — |a — 2|, եթե a = 4

20

բ)|3a — 6| — |2a — 1|, եթե a = -2

7

գ)|2a — 5| — |5a — 3|, եթե a = -6

-16

դ)|4a + 2| — |a|, եթե a = -2

8

3)Հաշվել արտահայտության արժեքը․

1.1/7

2.29/39

3.5

4.25

4)Լուծել խնդիրները․

1)8 տրակտոր 10 օրում վարում են 320 հա տարածք։

ա)3 տրակտորները 5 օրում քանի՞ հա տարածք կվարեն։

60

բ)8 տրակտորները քանի՞ օրում կվարեն 160 հա տարածք։

5

2)4 տրակտոր 7 օրում վարում են 280 հա տարածք։

ա)3 տրակտորները 4 օրում քանի՞ հա տարածք կվարեն։

10

բ)5 տրակտորները քանի՞ օրում կվարեն 300 հա տարածք։

5

3)5 տրակտոր 7 օրում վարում են 210 հա տարածք։

ա)2 տրակտորները 3 օրում քանի՞ հա տարածք կվարեն։

36

բ)4 տրակտորները քանի՞ օրում կվարեն 120 հա տարածք։

8

Գծելով y = x² ֆունկցիայի գրաֆիկը՝ ստացվում է նկարում պատկերված կորը։

Այդ գրաֆիկն անվանում են պարաբոլ: Պարաբոլի (0, 0) կետն անվանում են պարաբոլի գագաթ, իսկ գագաթից ձախ ու աջ ձգվող կորերը՝ պարաբոլի ճյուղեր:

Նշենք գրաֆիկի որոշ առանձնահատկություններ․

1)Ֆունկցիայի գրաֆիկն անցնում է կոորդինատների սկզբնակետով:

2)Բացի 0-ից, մնացած բոլոր կետերում ֆունկցիայի գրաֆիկը գտնվում է x-երի առանցքից վերև:

3)Գրաֆիկը համաչափ է y-երի առանցքի նկատմամբ:

4)Ֆունկցիան աճում է [0, +∞) միջակայքում:

5)Ֆունկցիան նվազում է (−∞, 0] միջակայքում:

6)Ֆունկցիայի որոշման տիրույթը R-ն է, իսկ արժեքների տիրույթը՝ [0, +∞):

Առաջադրանքներ․

1)Տրված x-երի համար գտե՛ք y-ի այնպիսի արժեք, որ (x, y) կետը լինի y = x² պարաբոլի վրա.
ա) x = 0 y=0
բ) x = 3 y=9
գ) x = — 3.2 y=3.2
դ) x = 111 y=222
ե) x = √5.5 y=5.5
զ) x = — √13 y=13
է) x = 2√3 y=23
ը) x = — 6√1.5 y=54

2)Հայտնի է, որ (x, y) կետը պատկանում է y = x² պարաբոլին: Գտե՛ք y-ի տրված արժեքի համար x-ի բոլոր հնարավոր արժեքները: Քանի՞ այդպիսի x կա.
ա) y = 0 x=0
բ) y = 25 x=5
գ) y = 196 x=96
դ) y = 2.89 x=1,445
ե) y = — 16 x=-8
զ) y = -2 x=1
է) y = 2 x=1
ը) y = 45 x= 22,5

3)Ո՞ր կետերում է տրված ուղիղը հատում y = x² ֆունկցիայի գրաֆիկը.
ա) y = 0
բ) y = 6
գ) y = — 1.1
դ) y = 64

4)Կառուցե՛ք y = x² ֆունկցիայի գրաֆիկի համաչափը x-երի առանցքի նկատմամբ:

5)Տրված է y = x² ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 9, բ) 0, գ) 15, դ)– 25 արժեքը:

1)Նկարում պատկերված է f(x) ֆունկցիայի գրաֆիկը: Պատկերե՛ք 2f(x) ֆունկցիայի գրաֆիկը։

1.

2.

3.

4.

2)Տրված է f(x) ֆունկցիայի գրաֆիկը։ Այն 1 միավորով վերև բարձրացնելով, այնուհետև y-ների առանցքի երկայնքով 2 անգամ ձգելով՝ ստացվում է g(x) ֆունկցիայի գրաֆիկը:
ա) Գծե՛ք g(x) ֆունկցիայի գրաֆիկը:

բ) g(x) ֆունկցիան արտահայտե՛ք f(x) ֆունկցիայի միջոցով։
գ) Գտե՛ք f(x) ֆունկցիայի զրոները:
դ) Գտե՛ք g(x) ֆունկցիայի փոքրագույն արժեքը:

3)Տրված է f(x) ֆունկցիայի գրաֆիկը: Այդ գրաֆիկը համաչափ արտապատկերելով (շրջելով) x-երի առանցքի նկատմամբ, այնուհետև y-ների առանցքի երկայնքով 2 անգամ սեղմելով՝ ստացվում է g(x) ֆունկցիայի գրաֆիկը:
ա) Գծե՛ք g(x) ֆունկցիայի գրաֆիկը:

բ) g(x) ֆունկցիան արտահայտե՛ք f(x) ֆունկցիայի միջոցով։
գ) Գտե՛ք g(x) ֆունկցիայի մեծագույն ու փոքրագույն արժեքները:

4)Տրված է f(x) ֆունկցիան, որի արժեքների տիրույթը [—3, 5] միջակայքն է:
Գտե՛ք ա)2/3f(x), բ) 1.8f(x) ֆունկցիայի արժեքների տիրույթը:

5)Տրված f(x) ֆունկցիան y-ների առանցքի երկայնքով սեղմեցին 2 անգամ, որից հետո համաչափ արտապատկերեցին աբսցիսների առանցքի նկատմամբ: Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց:

1)Գտնել 5 հայտարարով բոլոր կանոնավոր կոտորակների գումարը։

2

2)Գտնել 4 հայտարարով բոլոր կանոնավոր կոտորակների գումարը։

1.5

3)Գտնել 6 հայտարարով բոլոր կանոնավոր կոտորակների գումարը։

28.42

4)70-ը բաժանել 2:3 հարաբերությամբ։

28.32

5)60-ը բաժանել 1:4 հարաբերությամբ։

12.23

6)49-ը բաժանել 2:5 հարաբերությամբ։

7)Հաշվել արտահայտության արժեքը․

1/3

8)|-4| : |-2| + |-6| * 2 =

9)6 : |-3| — 2 : |-2| + 1 =

10)|-2| + |3| — |-4+1| =

11)Որդին տասը տարեկան է։ Հինգ տարի առաջ նա 7 անգամ փոքր էր հորից։

ա)Քանի՞ տարեկան է հայրը։

բ)Քանի՞ տարի հետո հայրը որդուց մեծ կլինի 2 անգամ։

12)Որդին ութ տարեկան է։ Երկու տարի առաջ նա 5 անգամ փոքր էր հորից։

ա)Քանի՞ տարեկան է հայրը։

բ)Քանի՞ տարի հետո հայրը որդուց մեծ կլինի 3 անգամ։