Իրական թվերը ենթարկվում են հետևյալ կանոններին՝
1 -ին կանոն: Ցանկացած երկու a և b իրարից տարբեր իրական թվերից մեկը մյուսից մեծ է: Այսինքն, ցանկացած a և b իրական թվերի համար տեղի ունի հետևյալ առնչություններից միայն մեկը՝a=b,a>b,a<b
Օրինակ․
10 և 15 թվերի համար ճիշտ է 10<15 անհավասարությունը, և սխալ են մյուս երկու առնչությունները՝ 10=15 և 10>15
2 -րդ կանոն: Ցանկացած երկու a և b իրարից տարբեր իրական թվերի միջև կա երրորդ թիվը: Այսինքն` եթե a<b, ապա գոյություն ունի այնպիսի c թիվ, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝ a<c<b
Օրինակ․
1.4 և 1.5 թվերի համար գոյություն ունի, օրինակ, 1.44 թիվը, այնպես, որ տեղի ունի հետևյալ երկկողմանի անհավասարությունը՝ 1.4<1.44<1.5
3 -րդ կանոն: Ցանկացած երեք a, b և c իրական թվերի համար, եթե a<b և b<c, ապա a<c:
Այս հատկությունը կոչվում է անհավասարությունների փոխանցելիության (տրանզիտիվության) հատկություն: Թվային առանցքի վրա կարելի է պատկերել այսպես:
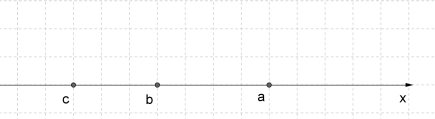
Օրինակ․
10/11<1 և 1<6/5 անհավասարություններից բխում է 10/11<6/5 անհավասարությունը:
Թվի գումարումը և թվով բազմապատկումը ՝
1 -ին հատկություն: Եթե a>b, ապա a+c>b+c
Եթե անհավասարության երկու մասերին գումարել կամ հանել միևնույն թիվը, ապա անհավասարության նշանը չի փոխվի:
Օրինակ․
3<12 ճիշտ անհավասարության երկու մասերին գումարելով −2 թիվը, կստանանք ճիշտ անհավասարություն՝ 1<10
2 -րդ հատկություն: Եթե a>b և k>0, ապա ak>bk
Եթե անհավասարության երկու մասերը բազմապատկել միևնույն դրական թվով, ապա անհավասարության նշանը չի փոխվի:
Օրինակ․
Գիտենք, որ 17,2<x<17,3: Գնահատենք 2x -ը:
Կրկնակի անհավասարությունը դրական 2 թվով բազմապատկելիս ստացվում է միանուն անհավասարություն (նշանները չեն փոխվում):
17,2⋅2<x⋅2<17,3⋅2
34,4<2x<34,6
3 -րդ հատկություն: Եթե a>b և k<0, ապա ak<bk
Եթե անհավասարության երկու մասերը բազմապատկել միևնույն բացասական թվով, ապա անհավասարության նշանը կփոխվի:
Օրինակ․
Հայտնի է, որ 17,2<x<17,3: Գնահատենք −2x-ը:
Կրկնակի անհավասարությունը բացասական −2 թվով բազմապատկելիս ստացվում է հականուն անհավասարություն (նշանները փոխվում են):
17,2⋅(−2)<x⋅(−2)<17,3⋅(−2)
−34,4>−2x>−34,6
−34,6<−2x<−34,4
Անհավասարումների գումարումն ու հանումը.
Եթե a>b և c>d, ապա a+c>b+d
Միանուն անհավասարությունները կարելի է գումարել:
Դիտարկենք երկու օրինակ:
Օրինակ`
1. Գիտենք, որ 1,2<x<1,3 և 17<y<18
Գնահատենք x+y -ը:
Եթե միանուն անհավասարությունները գումարել, ապա նշանները չեն փոխվի:

2. Գիտենք, որ 1,2<x<1,3 և 17<y<18
Գնահատենք x−y -ը:
Բազմապատկենք 17<y<18 կրկնակի անհավասարությունը −1 -ով, և փոխենք անհավասարության նշանները՝

Գումարելով առաջին անհավասարությունը ստացվածի հետ, ստանում ենք՝

Միանուն անհավասարությունների բազմապատկումը.
Եթե a−ն,b−ն,c−ն,d−ն դրական թվեր են և a>b,c>d, ապա ac>bd
Եթե դրական ձախ և աջ մասերով միանուն անհավասարումները բազմապատկել, ապա կստացվի միանուն անհավասարություն (նշանը չի փոխվի):
Դիտարկենք երկու օրինակ:
Օրինակ
1. Գիտենք, որ x<5 և y<11
Գնահատենք xy -ը:
Բազմապատկելով միանուն անհավասարությունները, ստանում ենք՝

2. Գիտենք, որ 1,2<x<1,3 և 2<y<3
Գնահատենք՝ xy -ը:
Բազմապատկելով միանուն անհավասարությունները, ստանում ենք միանուն անհավասարություն (նշանները չեն փոխվում)՝

Անհավասարության աստիճան բարձրացնելը.
Եթե a և b թվերը դրական են a<b, ապա an<bn, որտեղ n -ը բնական թիվ է:
Եթե դրական ձախ և աջ մասերով միանուն անհավասարումները բարձրացնել միևնույն բնական աստիճանի, ապա կստացվի միանուն անհավասարություն (նշանը չի փոխվի):
Օրինակ
1. Քանի, որ 2<3, ապա քառակուսի բարձրացնելով, ստանում ենք ևս մեկ ճիշտ անհավասարություն՝
22=4, 32=9
4<9
Առաջադրանքներ․
1)Նշեք նշված թվերից մեկից մեծ և մյուսից փոքր թիվ։ Պատասխանը գրեք կրկնակի անհավասարության տեսքով`
ա) 3 և 5;3>4>5
բ)-25 և-29;-25>-28>-29
գ) 2,4 և 2,404;2,4>2,5>2,404
դ) 2,5 և 2,6;2,5>2,55>2,6
ե)-3,71 և -3,72;
զ) -0,501 և 0,6:
2)Տրված ճշմարիտ անհավասարությունից ստացեք նոր ճշմարիտ անհավասարություն՝ գումարելով նրա երկու մասերին միևնույն թիվը՝
ա) 15 < 20
բ) 1,1 < 1,2
գ) 5 > 4
դ) 1,3 ≥ 1,2
ե) 2,5 < 3 ;
զ) 5 ≤ 6
3)Երկու ճշմարիտ անհավասարությունների հիման վրա կատարեք եզրակացություն։
Օրինակ 3 < 15 և 15 < 20, նշանակում է 3 < 20 :
ա)-5 < 0 և 0 < 2 ;
բ) 2 > 1 և 1 > 0
գ) -3,7 > -4 և — 4 > — 7
դ)-2 < 0 և 0 < 2
ե) 2,(1) > 2 և 2 > 1,(6)
զ) 0,(5) < 0,(6) և 0,(6) < 0,(67)
4)Բազմապատկեք ճշմարիտ թվային անհավասարությունները`
ա) 14 > 10 և 2 > 1
բ) 5 > 3 և 6 > 5
գ) 6 < 7 և 2 < 3
դ) 8 < 9 և 1 < 2
5)Գումարեք ճշմարիտ թվային անհավասարությունները՝
ա)14 > 11 և 10 > 9
բ)-2 > -3 և 3 > 2
գ)-6 < -5 և 2 < 3
դ)-8 < 0 և 8 < 9
6)Տրված ճշմարիտ անհավասարությունից ստացեք ճշմարիտ անհավասարություն, որում յուրաքանչյուր թիվ փոխարինված է իր հակադիրով։
Օրինակ, քանի որ 19 > 13, ապա -19 < -13։
ա)3 > 0
բ)5 > -1
գ)-9 < -1
դ)-5 < -1
ե)9 > -2
զ)0 < 3













