Рубрика: հանրահաշիվ

1)

(a⁵)²=(a²)⁵

(a³)⁴=(a²)⁶

(a⁶)⁷=(a²)²¹

2)

1.11*(2^7-12)=11*2^-5 =11*1/2⁵ =11*32

2.5*(3^15-11)=5*3⁴=5*27

1.a^-1        2.a¹

3.a⁴         4.a

5.a^-10       6.a⁹

7.a¹         8.a⁹

9.a^-3        10.a^-8

1.2⁷          2.5⁶

3.4 ⁵          4.7 ⁷

5.3 ¹³        6.6¹³

7.16⁶        8.9¹⁵

1.5/6²             2.2/2⁹          3.25/49⁴          4.m/a⁷          5.m/a⁸         6.n/a¹²

Թվային արտահայտությունը կազմվում է թվերից, թվաբանական գործողությունների նշաններից և փակագծերից:

Թվային արտահայտության գործողությունների արդյունքում ստացված թիվը կոչվում է թվային արտահայտության արժեք:

Եթե արտահայտության մեջ պատահում է բաժանում զրոյի վրա, ապա այդ արտահայտությունն արժեք (իմաստ) չունի: Զրոյի վրա բաժանել չի կարելի:  

(−3)²+5⋅0,2 թվային արտահայտության արժեքը հավասար է 10-ի:

(7−(−2)⁵+(6⋅4))0 արտահայտությունն արժեք չունի:

Եթե թվային արտահայտությունը պարունակում է նաև տառեր (կամ միայն տառեր), ապա այն կոչվում է հանրահաշվական արտահայտություն:

(−3)²+5x;3a+4b;(2x−6)/3 արտահայտությունները հանրահաշվական են:

Հանրահաշվական կոտորակ կոչվում է A/B տեսքի արտահայտությունը, որտեղ A-ն որևէ բազմանդամ է, իսկ B-ն՝ ոչ զրոյական բազմանդամ:

Հանրահաշվական կոտորակը բազմանդամի և ոչ զրոյական բազմանդամի քանորդ է:

x/(x−3);(b−1)/(b+6);(1+x³)/(x²+1);(y+2)/(y²−6y+6)արտահայտությունները հանրահաշվական կոտորակներ են:

Իմանալով իրական թվերի բազմապատկման կանոնը՝ սահմանենք իրական թվի ամբողջ ցուցիչով աստիճանը:

Եթե n-ը բնական թիվ է և a≠0, ապա՝

1. aⁿ=a⋅a⋅⋅⋅a n  անգամ

2. a⁻ⁿ=1/aⁿ

Օրինակ

4⁻³=1/4³=1/64

7⁻²=1/7²=1/49

Օգտվելով իրական թվերի բազմապատկման օրենքներից՝ դժվար չէ համոզվել, որ այս ձևով սահմանված ամբողջ ցուցիչով աստիճանն ունի հետևյալ հատկությունները՝ 

1.a^m⋅aⁿ=a^m+n

2.a^m/aⁿ=a^m−n

3.aⁿ⋅bⁿ=(a⋅b)ⁿ

4.aⁿ/bⁿ=(a/b)ⁿ

5.(aⁿ)^m=a^n⋅m

Առաջադրանքներ․

1)Հաշվե՛ք․

ա)5⁰ =1

բ)(-1/3)⁰ =1

գ)(-1,2)⁰ =1

դ)(-1)⁰ =1

2)Հաշվե՛ք․

ա)2⁴ / 2³ =2¹=2

բ)2⁴ / 2⁴ =2⁰=1

գ)(-0,3)⁴ / (-0,3)⁵ =(-0,3)^-1 =-1/0,3

դ)0,2⁷ / 0,2⁵ =0,2²=0,2

3)Գրե՛ք ամբողջ ցուցիչով աստիճանի տեսքով․

ա)2 · 2 · 2 =8

բ)2³ · 2⁵ =4⁸

գ)1 / 3² =3²

դ)4 =4

ե)0,5⁶/0,5⁷ =

զ)(-1/5)³ : (-1/5)⁷ =

4)Համեմատե՛ք․

ա)5⁰ = (-5)⁰

բ)5^-2 < 5²

գ)(-2)³ > (-2)⁰

5)Գրե՛ք ամբողջ ցուցիչով աստիճանի տեսքով․

ա)a³ · a⁴ =a⁷

բ)a⁴ · a =a⁵

գ)a¹³ : a⁶ =a⁷

դ)a⁴ · b⁴ =ab⁸

Լրացուցիչ աշխատանք (տանը).

1)Հաշվե՛ք․

ա)2⁴ / 2⁵ =2^-1

բ)2⁵ / 2⁷ =2^-2

գ)3⁵ / 3⁴ =3¹

դ)3¹⁰⁰ / 3¹⁰⁰ =3²⁰⁰

2)Գրե՛ք ամբողջ ցուցիչով աստիճանի տեսքով․

ա)1/3 =1/3

բ)1/3 · 3 · 3 · 3 =1/54

գ)5 =5

դ)1/16 =1/16

ե)1/25 =1/25

զ)2³ : 2³ =

է)9⁷/ 9⁵ =

3)Համեմատե՛ք․

ա)-3² և (-3)²

բ)(-2)⁴ և 2^-4

գ)-2⁴ և 2^-4

4)Գրե՛ք ամբողջ ցուցիչով աստիճանի տեսքով․

ա)a¹² : a =

բ)(a⁴)⁶ =

գ)(a²)⁵ =

դ)a⁷ · b⁷ =

Առաջադրանքներ․

1)Պարզեք՝ (-3;1) թվազույգը համակարգի լուծու՞մ է․

1)-3+1-3=-5  ոչ

2)-6-3-1=0 այո

1.-3-1+4=0  այո

2.-9+4+5=0 այո

2)Ցույց տվեք, որ (-2;1) թվազույգը համակարգի լուծում չէ․

1)-4x-1+5=0 այո

2)-2+1-3=0 այո

1)-4x+5y-1=0 այո

2)-6x-4=0 ոչ

3)a-ի և b-ի ի՞նչ արժեքների դեպքում (1;0) թվազույգը համակարգի լուծում է․

Դիցուք տրված է x և y անհայտներով գծային հավասարումների համակարգ՝

{a₁x+b₁y+c₁=0

{a₂x+b₂y+c₂=0

(x;y) թվազույգը կոչվում է համակարգի լուծում, եթե այն բավարարում է համակարգի հավասարումներից յուրաքանչյուրին:

Առաջին աստիճանի գծային հավասարմանը բավարարում են նրա գրաֆիկի՝ ուղիղ գծի վրա գտնվող բոլոր (x;y) կետերը:

Հետևաբար, եթե մենք ուզում ենք, որ բավարարվեն համակարգի երկու գծային հավասարումները միաժամանակ, ուրեմն պետք է փնտրել այնպիսի (x;y) կետեր, որոնք միաժամանակ պատկանում են երկու ուղիղներից յուրաքանչյուրին:

Այսպիսով, համակարգի լուծումները համակարգի հավասարումներով տրվող ուղիղների (գրաֆիկների) ընդհանուր կետերն են:

Օրինակ՝

1. Լուծենք հետևյալ համակարգը:

{x+2y−5=0,

{2x+4y+3=0

x+2y−5=0 հավասարման գրաֆիկն ուղիղ գիծ է: Կառուցենք այդ ուղիղը:  

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	5	0
y	0	2,5

xОy հարթության վրա կառուցենք գտնված (5;0) և (0;2.5) կետերը և դրանցով տանենք l1 ուղիղը:

2x+4y+3=0 հավասարման գրաֆիկը ևս ուղիղ գիծ է: 

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	−1,5	2,5
y	0	−2

xОy հարթության վրա կառուցենք գտնված (−1.5;0) և (2.5;−2) կետերը և դրանցով տանենք l2 ուղիղը:

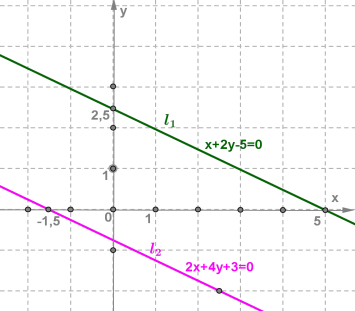
l1 և l2 ուղիղները զուգահեռ են և չունեն ընդհանուր կետեր:

Պատասխան՝ համակարգը լուծում չունի:   

Օրինակ՝

2. Լուծենք հետևյալ համակարգը:

{2x−y−5=0,

{2x+y−7=0

Համակարգի հավասարումները բերենք գծային ֆունկցիայի ընդհանուր տեսքին՝ y=2x−5 և y=−2x+7

y=2x−5 ֆունկցիայի գրաֆիկը ուղիղ գիծ է:

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	0	3
y	−5	1

xОy հարթության վրա կառուցենք գտնված (0;−5) և (3;1) կետերը և դրանցով տանենք l1 ուղիղը:

y=−2x+7 ֆունկցիայի գրաֆիկը ուղիղ գիծ է:

Գտնենք այս հավասարմանը բավարարող երկու կետ՝

x	0	1
y	7	5

xОy հարթության վրա կառուցենք գտնված (0;7) և (1;5) կետերը և դրանցով տանենք l2 ուղիղը:

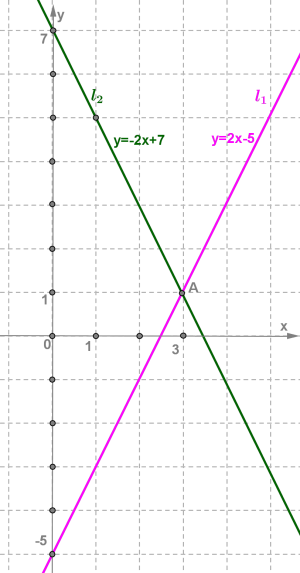
l1 և l2 ուղիղները հատվում են A կետում, որի կոորդինատները համակարգի միակ լուծումն են:

Պատասխան՝ (3;1)

Օրինակներում կիրառեցինք համակարգերի լուծման գրաֆիկական եղանակը:

Գրաֆիկական եղանակը հուսալի չէ, քանի որ միշտ չի հաջողվում ճշգրիտ գտնել հատման կետի կոորդինատները: Այդ պատճառով, խորհուրդ է տրվում գրաֆիկորեն գտնված կետը տեղադրել համակարգի հավասարումների մեջ և համոզվել, որ դրանք բավարարվում են:

Այսպիսով, գալիս ենք հետևյալ եզրակացություններին:

1. Համակարգի հավասարումներով տրված ուղիղները կարող են հատվել մեկ կետում: Այդ կետի կոորդինատները համակարգի միակ լուծումն են:

2. Համակարգի հավասարումներով տրված ուղիղները կարող են լինել զուգահեռ և չհատվել: Այս դեպքում համակարգը լուծում չունի:

3. Համակարգի հավասարումներով տրված ուղիղները կարող են համընկնել: Այս դեպքում համակարգն ունի անվերջ թվով լուծումներ:

Առաջադրանքներ․

Հավասարումների համակարգը լուծել գրաֆիկական եղանակով․

1)

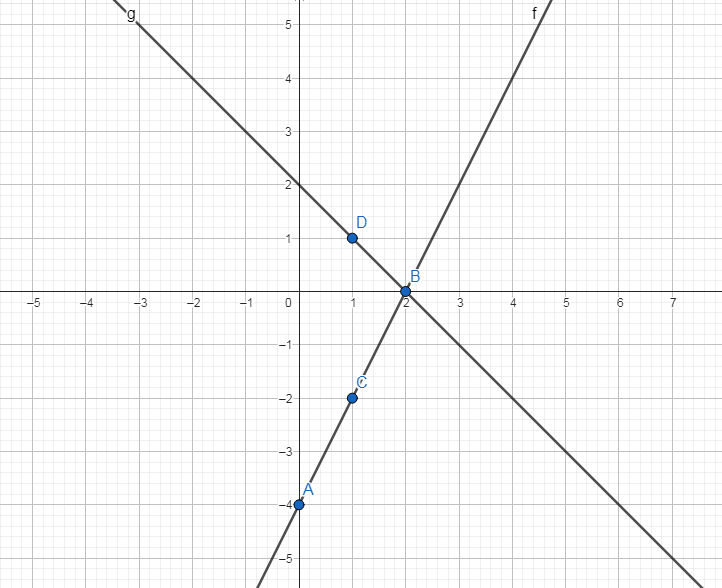
x=0 y=-4

x=1y=-2

x=0y=-2

(2,0)

2)

x=0y=2

x=1y=1

x=1y=2

x=0y=3

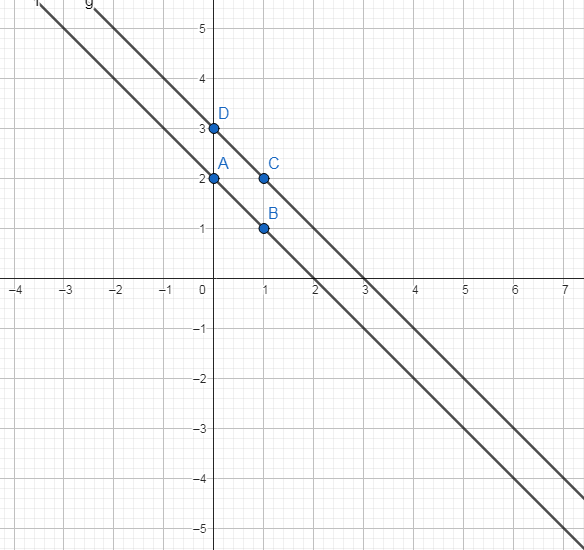
3)

4)

5)

Լրացուցիչ աշխատանք (տանը)․

Հավասարումների համակարգը լուծել գրաֆիկական եղանակով․

1)

2)

3)

4)

Օրինակ (հնագույն) Հանդիպեցին երկու հովիվ՝ Հովհաննեսը և Պետրոսը: Հովհաննեսն ասում է Պետրոսին. «Տուր ինձ մի ոչխար, և ինձ մոտ կլինի երկու անգամ ավելի ոչխար, քան քեզ մոտ»: Իսկ Պետրոսը նրան պատասխանում է. «Ոչ, ավելի լավ է դու տուր ինձ մի ոչխար, և մեզ մոտ կլինեն հավասար թվով ոչխարներ»: Քանի՞ ոչխար ուներ նրանցից յուրաքանչյուրը:

Լուծում: Դիցուք Հովհաննեսն ուներ x ոչխար, իսկ Պետրոսը՝ y ոչխար: Եթե Պետրոսը Հովհաննեսին տար մեկ ոչխար, ապա Պետրոսի մոտ կմնար (y-1) ոչխար, իսկ Հովհաննեսի մոտ կլիներ (x+1) ոչխար:

Բայց այդ դեպքում Հովհաննեսի մոտ երկու անգամ շատ ոչխար կլիներ, քան Պետրոսի մոտ: Հետևաբար

                                        x+1=2(y-1):

Իսկ եթե Հովհաննեսը Պետրոսին մեկ ոչխար տար, ապա Հովհաննեսի մոտ կմնար (x-1) ոչխար, իսկ Պետրոսի մոտ կդառնար (y+1) ոչխար: Բայց այդ դեպքում նրանք կունենային հավասար թվով ոչխարներ: Հետևաբար

                                      x-1=y+1:

Այս երկու հավասարումներից կազմենք համակարգ՝

Համակարգն էլ լուծելով մեզ արդեն ծանոթ տեղադրման կամ գումարման եղանակով՝ կստանանք, որ x=7; y=5: Այսպիսով, Հովհաննեսն ունի 7 ոչխար, իսկ Պետրոսը՝ 5 ոչխար:

Առաջադրանքներ․

1) 

ա) Երկու թվերի գումարը 10 է, իսկ տարբերությունը՝ 4: Գտեք այդ թվերը:

{x+y=10
{x-y=4

10+4=14

=>x=7

7+3=10

=>y=3

բ) Երկու թվերի գումարը 21 է, իսկ տարբերությունը՝ 9: Գտեք այդ թվերը:

{x+y=21
{x-y=9

21+9=30

=>x=15

15+6=21

=>6

2) Մի թիվը 2 անգամ մեծ է մյուսից: Եթե այդ թվերից փոքրը մեծացվի 4 անգամ, իսկ մեծը՝ 2 անգամ, ապա նրանց գումարը հավասար կլինի 44: Գտեք այդ թվերը:

x=2y

4y+2x=44

8y=44

y=5.5

5.5×4=22

22:12=11

x=11

3) Տրված են երկու թվեր։ Եթե առաջին թիվը բազմապատկենք 2-ով, ապա ստացված թիվը 1-ով մեծ կլինի երկրորդից, իսկ եթե երկրորդ թիվը բազմապատկենք 2-ով, ապա ստացված թիվը 7-ով մեծ կլինի առաջինից։ Գտեք այդ թվերը։

2x=1+y

2y=7+y

Լրացուցիչ աշխատանք (տանը)․

1)

 ա) Մի թիվը 6-ով մեծ է մյուսից: Այդ թվերի գումարը հավասար է 40-ի: Գտեք այդ թվերը:

40:2=20

20-6=14

x=20

y=14

բ) Մի թիվը 15-ով փոքր է մյուսից: Գտեք այդ թվերը, եթե նրանց գումարը 23 է:

23:2=11.5

11.5+15=26.5

x=11.5

y=26.5

2) Մի թիվը 7-ով մեծ է մյուսից: Եթե փոքր թիվը մեծացվի 2 անգամ, իսկ մեծը՝ 6 անգամ, ապա նրանց գումարը կդառնա 31: Գտեք այդ թվերը:

x=7y

y2+x6=8

7y=8

Լուծեք հավասարումների համակարգը․

2x+4y-6=0

2x-3y+8=0

7y-14=0

7y=14

y=2

x+4-3=0

x=-1

8x+4y-32=0

3x+4y-7=0

5x-25=0

5x=25

x=5

10+y-8=0

y-2

Երկու անհայտներով երկու հավասարումների համակարգի լուծման գումարման (գործակիցների հավասարեցման) եղանակի ալգորիթմը:

1. Հավասարեցնել (եթե անհրաժեշտ է) փոփոխականներից մեկի գործակիցների մոդուլները:
2. Գումարել կամ հանել հավասարումները: Լուծել ստացված մեկ փոփոխականով հավասարումը և գտնել անհայտներից մեկը:  

3. Երկրորդ քայլում գտած արժեքը տեղադրել հավասարումներից որևէ մեկի մեջ և գտնել համակարգի երկրորդ փոփոխականի արժեքը:  

4. Գրել պատասխանը: 

Օրինակ՝ Լուծել հավասարումների համակարգը՝ 

Գումարենք հավասարումները՝

x-ի գտած արժեքը տեղադրենք հավասարումներից որևէ մեկի մեջ, օրինակ՝ երկրորդի և գտնենք y-ը՝

Առաջադրանքներ․

Լուծեք հավասարումների համակարգը․

1)

y-4=0

y=4

x+4+1=0

x+5=0

x=-5

2)

x-5=0

x=5

20+y-2=0

y=-18

3)

y-7=0
y=7

x-7=0

x=7

4)

Առաջադրանքներ․

y=11-2x

3x-11+2x=9

5x=20

y=11-8=3

y=5-2y

10-4y+y=-5

-5y

Երկու անհայտներով երկու հավասարումների համակարգի լուծման տեղադրման եղանակի ալգորիթմը:

1. Համակարգի հավասարումներից որևէ մեկից (սովորաբար ավելի պարզից) արտահայտել փոփոխականներից մեկը մյուսի միջոցով, օրինակ՝ առաջին հավասարումից արտահայտել x-ը y-ի միջոցով:

2. Ստացված արտահայտությունը տեղադրել մյուս (երկրորդ) հավասարման մեջ, օրինակ՝ x-ի փոխարեն:

3. Լուծել մեկ անհայտով հավասարումը, օրինակ՝ y-ի նկատմամբ (գտնել y-ը ),

4. Երրորդ քայլում գտնված y-ի արժեքը տեղադրել y-ի փոխարեն՝ առաջին քայլում ստացված հավասարման մեջ և գտնել x-ը:

5. Գրել պատասխանը:

Օրինակ

Լուծել հավասարումների համակարգը՝

1) Առաջին հավասարումից ստանում ենք՝

x−2y=3

x=3+2y

2) Ստացված արտահայտությունը տեղադրում ենք երկրորդ հավասարման մեջ՝ x-ի փոխարեն՝

5⋅x+y=4

5⋅(3+2y)+y=4

3) Լուծենք ստացված հավասարումը և գտնենք y-ը՝

5⋅(3+2y)+y=4

15+10y+y=4

10y+y=4−15

11y=−11

y=−1

4) Տեղադրենք y-ի գտնված արժեքը առաջին քայլում ստացած հավասարման մեջ՝ y-ի փոխարեն և գտնենք x-ը՝

x=3+2⋅y

x=3+2⋅(−1)

x=3−2

x=1

5) Պատասխան՝ (1;−1)

Առաջադրանքներ․

1)

x=2y

2.2y-3y-7=0

4y-3y-7=0

y=7

2)

x=-5y

-5y.3+7y-16=0

-15y+7y-16=0

-8y=16

y=-7

3)

y=3x

x-6x+10=0

-5x=-10

x=2

4)