Մանվել Դավթյան

բարությունը աշխարհում ամենա լավ բաներից մեկն է եթե մարդ շատ բարի լինի կօգնի մարդկանց որպիսղի մարդիկ այդ դժվարությունից դուրս գան իսկ եթե մարդը եղավ չար ճիշտ հակառակը կվարվի այդ մարդու հետ պետք չե լինել չար պետպ է լինել բարի իմ կողմից ձեզ խորհուրդ միշտ եղեք բարի

Տնային

1. Որոշե՛ք պրոտոնների, նեյտրոնների և էլեկտրոնների քանակը և ատոմային միջուկի լիցքը հետևյալ տարրերի համար՝ լրացնելով աղյուսակը.

1) S, O, B, Ba, Si

2)Mn , Ν, Zn, As

2. Հաշվե՛ք, նյութի՝ KOH հարաբերական մոլեկուլային զանգվածը և նյութի բաղադրության մեջ առկա տարրերի զանգվածային բաժինները:

Mr=(KON)=2Ar(K)+(O)+(N)=

Սխալ կազմած  պատճառական բայերն ուղի՛ր:

Քնեցնել, հաշտեցնել, լռացնել, ուտացնել-կերակրել, լսեցնել, ճերմակեցնել, կարմրացնել, վախացնել-վախեցնել, աշխատացնել, հնչեցնել, պարզեցնել, ցավեցնել, վստահացնել-վստահեցնել, ծառայացնել, ապրացնել:

2. Տրված բայերը պատճառակա՛ն դարձրու: Պատճառական դարձնող մասնիկն ընդգծի՛ր:

Օրինակ`

ա) զգալ- զգացնել

բ) մեծանալ – մեծացնել,(մեծացրի)

գ) հագնել- հագցնել (հագցրի)
ա) Խաղալ-խաղացնել, դողալ-դողացնել, եռալ-եռացնել, թվալ-թվացնել, հավատալ-հավատացնել:
բ) Փոքրանալ-փոքրեցնել, լավանալ-լավացնել, վատանալ-վատացնել, բարեկամանալ-բարեկամացնել, թշմանալ-թշնամացնել, մանրանալ-մանրացնել, հզորանալ-հզորացնել, բարձրանալ-բարձրացնել, քարանալ-քարացնել:
գ) Հասնել-հասցնել, թռչել-թռցնել, տեսնել-, փախչել, փակչել, կպչել-կապել:

Հարգելի՛ սովորողներ, այս շաբաթ ներկայացնելու եք․

• Ժապավենաձև որդերի դաս
• Հին դասագիրք- էջ՝116-117

Լրացուցիչ առաջադրանք, պատասխանել հարցերին

Մարտի 5-11

Սիրելի՛ սովորողներ, այս շաբաթ ներկայացնելու եք հետևյալ թեմաները․

• Անձրևորդի արտաքին և ներքին կառուցվածքը

1. Համացանցից գտնել  10 հետաքրքիր փաստեր սողունների մասին։
2. Հայաստանում տարածված ի՞նչ սողուններ են ձեզ հայտնի, ներկայացնել մի քանի օրինակ։ օրինակ օձը և մողեսը
3. Ներկայացնել սողունների բազմացումը-նրանք բազմանւոմ են սեռական ճանապարհով

Սողունների բազմացումը և զարգացումը

Սողունների սեռական օրգանները և դիմորֆիզմը

Բոլոր սողունները բաժանասեռ կենդանիներ են և բազմանում են ներքին բեղմնավորմամբ: Սողունների բազմացման օրգանները կառուցվածքով շատ նման են երկկենցաղների բազմացման օրգաններին:

Արուն ունի երկար զույգսերմնարաններ, որոնք սերմնածորաններով բացվում են կոյանոցի մեջ:

Էգը ունի զույգ ձվարաններ, որոնք ձվատարներով բացվում են կոյանոցի մեջ:

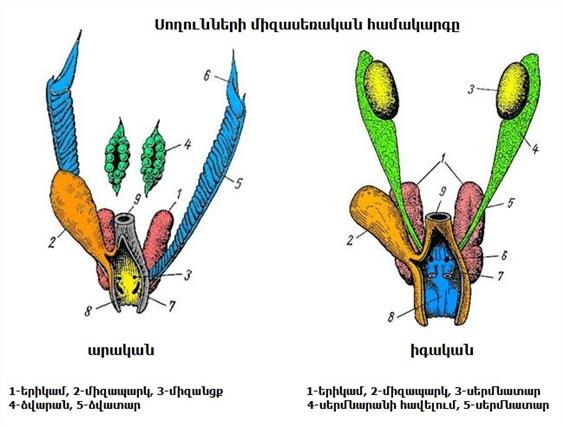
Բազմացման շրջանում զարգացած ձվաբջիջը բեղմնավորվում է սպերմատոզոիդի հետ հենց էգի օրգանիզմում:

Սողունների մոտ լավ արտահայտված է սեռական դիմորֆիզմը: Արուները ունեն վառ գունավորում, ավելի խոշոր են և գրավում են էգերին: Արուներին բնորոշ է նաև մեկ այլ առանձնահատկություն. նրանք բազմացման ընթացքում, օրինակ՝ որոշ մողեսներ, մաշկի վրա, մեջքի երկարությամբ կարող են ձեռք բերել լրացուցիչ կատարներ, թմբուկներ, հավելյալ երանգներ: Այդ ամենը բարձրացնում է արուի գրավչությունը էգի մոտ:

Տարբերում ենք սողունների բազմացման և զարգացման 5 հիմնական փուլ.

• ձվազատում
• բեղմնավորում 
• ձվի զարգացում
• ձվադրում
• ուղղակի զարգացում

Ձվազատում

Էգի սեռական օրգաններում՝ ձվարաններում, զարգանում են իգական սեռական բջիջները՝ ձվաբջիջները: Ձվարանից դուրս գալուց հետո ձվաբջիջը ընկնում է ձվատարի վերին, ձագարաձև լայնացած մասը: Ձվատարը ձգվում է մինչև կոյանոց և բացվում դրա մեջ: Կատարվում է հասունացած ձվաբջջի ձվազատում, որը արդյունքում մնում է էգի օրգանիզմում:

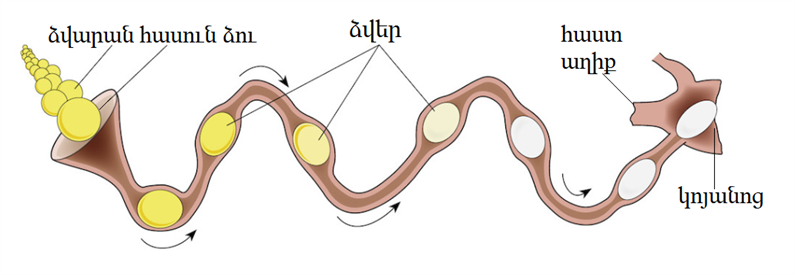
Բեղմնավորում

Գարնանը, երբ եղանակը տաքանում է, սկսվում է սողունների բազմացման շրջանը: Զուգավորման ժամանակ արուն սերմնաբջիջները լցնում է էգի կոյանոցը: Կոյանոցից շարժուն սպերմատոզոիդները ձվատարով բարձրանում և թափանցում են ձվաբջիջների մեջ: Ձվատարներում կատարվում է բեղմնավորում: Բեղմնավորումից ձևավորվում է զիգոտ: Զիգոտից սկիզբ է առնում սաղմնավորումը: 

Ձվի զարգացում

Բեղմնավորված ձվաբջիջը ձվատարով անցնելու ընթացքում պատվում է մագաղաթանման, ճկուն թաղանթով, օրինակ՝ օձերի և մողեսների մոտ: Կոկորդիլոսների և կրիաների բեղմնավորված ձվաբջիջները պատվում են կրային կճեպով: Ձվատարով շարժվելու ընթացքում կատարվում է բեղմնավորված ձվաբջջից ձվի զարգացման գործընթացը, որը ավարտին է հասնում կոյանոցում:

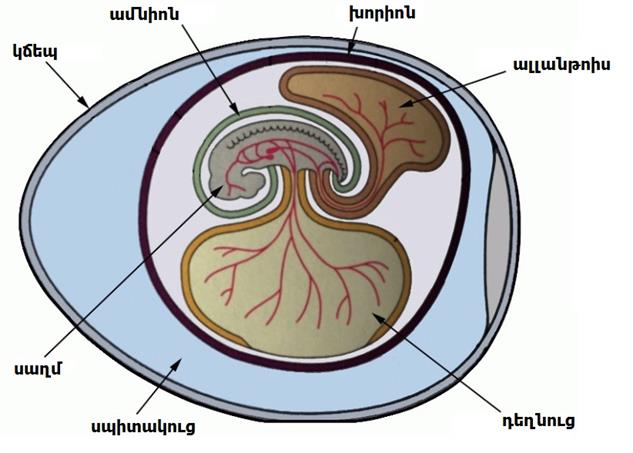
Սողունների ձուն հարուստ է դեղնուցով և ունի ցամաքի վրա սաղմի զարգացումն ապահովող հարմարանքներ:

Ձվի կառուցվածքային մասերն են.

• արտաքին ամուր թաղանթ
• սաղմնային թերթիկներ
• դեղնուցապարկ
• սաղմ

Դեղնուցի բաղադրության մեջ կան սաղմի աճման համար անհրաժեշտ բոլոր սննդարար նյութերը: Ձվի թաղանթները պաշտպանում են սաղմը արտաքին ազդեցությունից: Կճեպը ծակոտկեն է, որի շնորհիվ ձուն կատարում է նյութափոխանակություն: Ձվի մեջ՝ սաղմի շուրջ, զարգանում են սաղմնային թաղանթներ. դրանցից մեկը՝ ամնիոնը լցված է հեղուկով և ստեղծում է սաղմի զարգացման համար անհրաժեշտ ջրային միջավայր: Երկրորդ թաղանթը՝ ալլանթոիսը, հարուստ է արյունատար անոթներով և ապահովում է սաղմի շնչառությունն ու արտաթորությունը: Երրորդ թաղանթը՝ խորիոնը, սահմանազատում է սաղմնային մարմինը սպիտակուցային մարմնից և ապահովում դրանց միջև նյութափոխանակությունը: Սպիտակուցը հիմնական կիրառելի սննդային միջավայրն է, որից սաղմը ի վիճակի է կլանել պիտանի նյութեր և արտազատել արգասիքներ:Ձվադրում

Սողունները ձվերը դնում են ավազի, հողի մեջ, քարերի արանքում, տերևների տակ: Որոշ տեսակների ձվերը մնում են ձվատարում մինչև զարգացման ավարտը: Այդ դեպքում ձագերը դուրս են գալիս ձվերից անմիջապես ձվադրման պահին: Բազմացման այս ձևը կոչվում է ձվակենդանածնություն: Որոշ տեսակների սաղմը զարգանում է մոր ձվատարին ամրացած և պատված չէ ձվային թաղանթներով: Բազմացման այս ձևը կոչվում է կենդանածնություն: Որոշ սողունների արուներն ընդհանրապես չեն հանդիպում, և էգերը բազմանում են առանց բեղմնավորման՝ կուսածնությամբ:

Ուղղակի զարգացում

Լրիվ ձևավորված սաղմը, որը ամբողջական ձևավորված օրգանիզմ է, իր դնչի վրա գտնվող ատամիկով պատռում է ձվի թաղանթը և դուրս գալիս արտաքին միջավայր: Սողունների զարգացումը ուղղակի է՝ առանց կերպարանափոխության: Ձագերը ծնողների խնամքի կարիքը չեն զգում:

Կետերը փոխարինի՛ր տրված բայերի ենթադրական եղանակի համապատասխան ձևերով:

 Եթե թույլ տան իրենց ուզածն անել, նրանք անտառն էլ կվերացնեին զորքի, ու բոլոր ծառերը շարք կգանգնեցն էի  (վերածել, կանգնեցնել)
 Հենց որ սահմանին մոտենաք, ձեզ հարց ու փորձ անեին ձեր անցյալի ու նպատակների մասին: (հարցուփորձ անել)
Թե որ գտնես այդ բույսի սերմերը, ջրի մեջ … ու … մինչև ծլեն: (դնել, թողնել)
Եթե կենդանիների կերի մեջ մեծ քնակությամբ արևքուրիկ լինի, կենդանին կթունավորվեր ու կհիվանդանար (թունավորվել, հիվանդանալ)

Եթե ժամանակին չմտածեն կենդանիների կերի մասին, ձմռանը շատ դժվար  կլինեին կեր հայթաթելը: (լինել)

2. Տրված նախադասությունները լրացրո՛ւ հարկադրական եղանակի համապատասխան  բայերով:

Վատ աշխատող շարժիչներն անպայման պիտի,  թե չէ թունավորում են օդը:
Մեր քաղաքում սաղարթավոր ծառեր …պիտի, որ աղմուկը կլանեն, օդը մաքրեն փոշուց ու վնասակար նյութերից:
Մարդիկ ..պիտի., որ կենդանի բնությունը պահպանելը իրենց ամենակարևոր գործն է:
Ամեն մեկը դիմացինի համար ..պիտի.. այն, ինչ կուզեր, որ իր համար անեն մարդիկ:
Բնության գեղեցկությունը պահպանելու համար հանքերի շահագործումը ..պիտի.:

Գլխիվայր են ծառերն աճում,
Եվ ջրվեժներն ալեփրփուր
Դեպի երկինք ենշառաչում։

Սարը սարից ամպ է խլում,
Ջուր է խմում ձորը ձորից,
Երկնքի մեջ արտ է ծլում,
Ու երկինք է բուսնում հողից…

Այս իմ հրաշք աշխարհն է, ուր
Շողքը տեր է, շվաքը՝ հյուր։

Գրի՛ր մգեցված բառերի բացատրությունը:ալլեփրփուր-սպիտակ ալիքներ

շառաչում-ջրի ձայն

շվաքը-

 Ինչպիսինն է Սահյանի աշխարհը: Մի փոքր տարորինակ էր

,,Իմ աշխարհը,, վերնագրով շարադրություն գրի՛ր: 

1)Նայիր գրաֆիկին և գտիր մեկ ժամում անցած ճանապարհը․

110կմ․

2)Այս գրաֆիկը նկարագրում է ավտոմեքենայի անցած ճանապարհը որոշակի ժամանակահատվածների ընթացքում: 

 Քանի՞ ժամում ավտոմեքենան կանցնի 550 կմ-ը:

5 ժամում կանցնի 550 կմ

3)Տրված է ապրանքի վաճառքի եկամուտի կախվածության գրաֆիկը ապրանքի քանակից:

Լրացրու բերված աղյուսակի դատարկ պատուհանները:

Քանակ (կգ)	Եկամուտ (դրամ)
9	900
9	900

4)Շուկայում վաճառեցին 11 կգ տանձ: Պարզիր վաճառողի եկամուտը:

1100

5)Օդի ջերմաստիճանը չափել են մեկ օրվա ընթացքում։Չափումների արդյունքները ներկայացված են հետևյալ աղյուսակում․

Կառուցե՛ք օրվա ընթացքում օդի ջերմաստիճանի փոփոխության գրաֆիկը։

Սահյան

Ամպրոպից հետո

Երկինքն ավելի կապույտ է լինում,

Խոտերն ավելի կանաչ են լինում

Ամպրոպից հետո։

Ամպրոպից հետո

Ճերմակ շուշանը ավելի ճերմակ,

Կակաչն ավելի կարմիր է լինում

Եվ մեղրածաղիկն՝ ավելի դեղին։

Ամպրոպից հետո

Սարերն ավելի բարձր են երևում,

Խոր են երևում ձորերն ավելի,

Եվ տափաստաններն՝ ավելի արձակ։

Ծառերն ավելի խոնարհ են լինում

Ամպրոպից հետո,

Եվ հավքերը մեր գլխավերևում

Իրար կանչում են ավելի սրտով.

Ամպրոպից հետո

Բարի է լինում արևն ավելի,

Եվ մենք ավելի սիրով ենք իրար

Բարի լույս ասում։

Ամպրոպից հետո աշխարհը և դու

Հասկանալի եք լինում ավելի…

Հարցեր և առաջադրանքներ՝

1. Գրավոր պատմի՛ր բանաստեղծությունը: