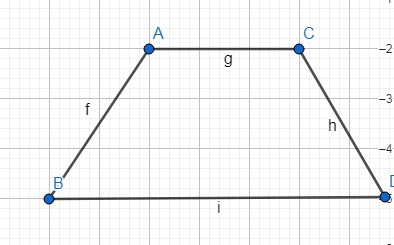
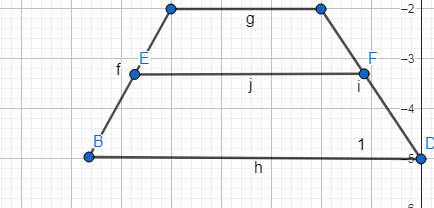
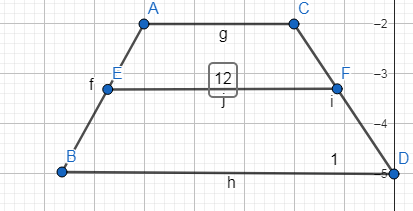
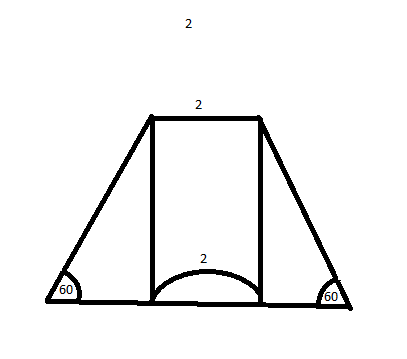
Ուղղանկյուն կոչվում է այն զուգահեռագիծը, որի բոլոր անկյունները ուղիղ են:

Ուղղանկյան հատկությունները․
Քանի որ ուղղանկյունը զուգահեռագիծ է, ապա այն ունի զուգահեռագծի բոլոր հատկությունները:
1. Ուղղանկյան հանդիպակաց կողմերը հավասար են՝ AB=CD, BC=AD
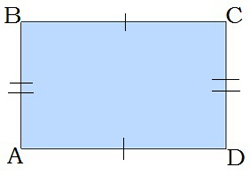
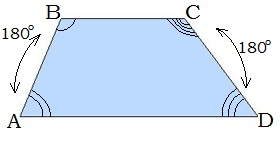
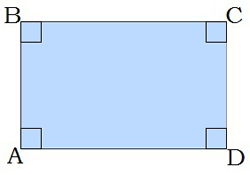
2. Ուղղանկյան յուրաքանչյուր անկյուն 90° է:
Հետևաբար, հանդիպակաց անկյունները հավասար են և կողմին առընթեր անկյունների գումարը 180° է:
3. Ուղղանկյան անկյունագծերը հատման կետով կիսվում են՝ BO=OD AO=OC
Նաև՝ BO=OD=AO=OC (տես, միայն ուղղանկյուններին բնորոշ, վեցերորդ հատկությունը) :

4. Անկյունագիծը ուղղանկյունը բաժանում է երկու հավասար ուղղանկյուն եռանկյունների:
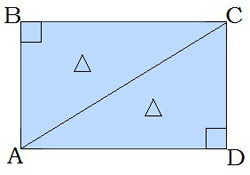
5. Անկյունագծին առընթեր խաչադիր անկյունները հավասար են:

Միայն ուղղանկյուններին բնորոշ հատկություն․
6. Ուղղանկյան անկյունագծերը հավասար են՝ BD=AC

Առաջադրանքներ․
1)Ուղղանկյան անկյունագծերի հատման կետի հեռավորությունը մեծ կողմից 4սմ է, իսկ փոքր կողմից՝ 6սմ։ Գտեք ուղղանկյան պարագիծը։

12+8=20
2)Գտեք ABCD ուղղանկյան պարագիծը, եթե A անկյան կիսորդը տրոհում է՝
ա)BC կողմը 45,6սմ և 7,85սմ երկարությամբ հատվածների

բ)DC կողմը 2,7դմ և 4,5դմ երկարությամբ հատվածների

4,5*3=13,5
7,5*2=15
7,5+4,5+4,5+15=31.5
13,5+31,5=45
3)ABCD ուղղանկյան անկյունագծերը հատվում են O կետում։ Գտեք AOB եռանկյան պարագիծը, եթե <CAD = 30o, AC = 12սմ։
30+12=42
Լրացուցիչ աշխատանք (տանը).
1)Ուղղանկյան կից կողմերից մեկը 10սմ է, իսկ մյուսը՝ 13սմ։ Գտե՛ք ուղղանկյան պարագիծը։
10+10+13+13=46
2)ABCD ուղղանկյան AB կողմը 6սմ է, իսկ BDA անկյունը՝ 30o։ Գտե՛ք AC անկյունագիծը։
6+30=36
3)ABCD ուղղանկյան անկյունագծերը հատվում են O կետում, E-ն AB կողմի միջնակետն է, <BAC = 50o։ Գտեք <AOE-ն։